题目内容
| sin2002°sin2008°-cos6° |
| sin2002°cos2008°+sin6° |
A、-
| ||
B、
| ||
| C、-tan28° | ||
| D、tan28° |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:本题可以先利用诱导公式将角转化到0~2π,再将6°角拆成两角之差后,利用两角和的正、余弦公式进行化简,得到本题结论.
解答:
解:
=
=
=
=
=-
=-
.
故选A.
| sin2002°sin2008°-cos6° |
| sin2002°cos2008°+sin6° |
=
| sin(5×360°+202°)sin(5×360°+208°)-cos6° |
| sin(5×360°+202°)cos(5×360°+208°)+sin6° |
=
| sin202°sin208°-cos(208°-202°) |
| sin202°cos208°+sin(208°-202°) |
=
| sin202°sin208°-[cos202°cos208°+sin202°sin208°] |
| sin202°cos208°+sin208°cos202°-cos208°sin202° |
=
| -cos202°cos208° |
| sin208°cos202° |
=-
| 1 |
| tan208° |
=-
| 1 |
| tan28° |
故选A.
点评:本题考查了三角函数诱导公式、两角和与差的正弦、余弦公式,还考查了化归转化的数学思想,本题难度不大,属于基础题.

练习册系列答案
相关题目
设全集U=R,M={x|x<-2或x>2},N={x|x<1或x≥3}都是U的子集,则图中阴影部分所表示的集合是( )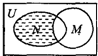

| A、{x|-2≤x<1} |
| B、{x|-2≤x≤2} |
| C、{x|1<x≤2) |
| D、{x|x<2} |
已知A={x|y=x2-1},B={y|y=x2-1},则A∩B( )
| A、∅ | B、A | C、B | D、R |