题目内容
过球O表面上一点A，引三条长度相等的弦AB、AC、AD，且两两夹角都为60°，若球半径为R，求弦AB的长度．
考点：球内接多面体
专题：计算题,空间位置关系与距离
分析：可设棱长为x、列出方程求解．关键就是确定出球心的位置．
解答：
解：如图，在正四面体ABCD中、作AO1⊥底面BCD于O1，则O1为△BCD的中心．
∵OA=OB=OC=OD=R，∴球心O在底面的射影也是O1，于是A、O、O1三点共线．
设正四面体ABCD的棱长为x，
则AB=x，BO1=
x，AO1=
x，
∵OO1=
，
又OO1=AO1-AO=
x-R，
由此解得x=
R，故正四面体ABCD的棱长，即弦AB的长度为
R．
∵OA=OB=OC=OD=R，∴球心O在底面的射影也是O1，于是A、O、O1三点共线．
设正四面体ABCD的棱长为x，
则AB=x，BO1=
| ||
| 3 |
| ||
| 3 |
∵OO1=
R2-
|
又OO1=AO1-AO=
| ||
| 3 |
由此解得x=
2
| ||
| 3 |
2
| ||
| 3 |
点评：①一个多面体的所有顶点在一个球面上，则称这个多面体内接于一个球，这个球也叫做多面体的外接球；②有关外接球的问题常常利用它的轴截面来解决．
练习册系列答案
相关题目
设全集U=R，M={x|x＜-2或x＞2}，N={x|x＜1或x≥3}都是U的子集，则图中阴影部分所表示的集合是（ ）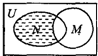
| A、{x|-2≤x＜1} |
| B、{x|-2≤x≤2} |
| C、{x|1＜x≤2） |
| D、{x|x＜2} |
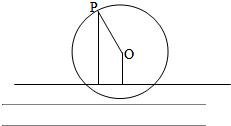如图是一个半径为3米的水轮，水轮圆心O距离水面2米，已知水轮每分钟转动四圈，水轮上的点P相对于水面的高度y（米）与时间x（秒）满足函数关系y=Asin（ωx+φ）+2（A＞0，ω＞0，φ∈（-用反证法证明命题：若p则q．其第一步是反设命题的结论不成立，这个正确的反设是（ ）
| A、若p，则￢q | B、若￢p，则q |
| C、￢p | D、￢q |