题目内容
若关于x的不等式ax2-(a+1)x+1<0(a∈R)的解集为(
,1),则a的取值范围为( )
| 1 |
| a |
| A、a<0,或a>1 | B、a>1 |
| C、0<a<1 | D、a<0 |
考点:一元二次不等式的解法
专题:计算题,不等式的解法及应用
分析:ax2-(a+1)x+1<0即(ax-1)(x-1)<0,由题意可知
,解出即可.
|
解答:
解:ax2-(a+1)x+1<0即(ax-1)(x-1)<0,
由关于x的不等式ax2-(a+1)x+1<0(a∈R)的解集为(
,1),得
,解得a>1,
故选:B.
由关于x的不等式ax2-(a+1)x+1<0(a∈R)的解集为(
| 1 |
| a |
|
故选:B.
点评:该题考查一元二次不等式的解法,属基础题,正确理解“三个二次”间的关系是解题关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
函数f(x)=2alog2x+a•4x+3在区间(
,1)上有零点,则实数a的取值范围是( )
| 1 |
| 2 |
A、a<-
| ||||
B、a<-
| ||||
C、-
| ||||
D、a<-
|
函数f(x)=lg|x|-sinx的零点个数为( )
| A、8 | B、6 | C、5 | D、3 |
已知变量x,y满足约束条件
,则z=2x+y的最小值为( )
|
| A、0 | B、1 | C、4 | D、6 |
已知
=(-3,4)与
=(6,x)共线,则x=( )
| a |
| b |
| A、8 | ||
| B、-8 | ||
C、
| ||
D、-
|
在等差数列{an}中,已知a2+a10=16,则a4+a8=( )
| A、12 | B、16 | C、20 | D、24 |
圆锥的底面半径为1,侧面展开图是一个半圆,则此圆锥的表面积为( )
| A、6π | ||||
| B、5π | ||||
| C、3π | ||||
D、
|
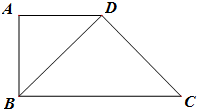 如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起.设折起后点A的位置为A′,并且平面A′BD⊥平面BCD.给出下面四个命题:
如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起.设折起后点A的位置为A′,并且平面A′BD⊥平面BCD.给出下面四个命题: