题目内容
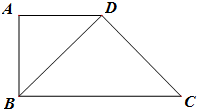 如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起.设折起后点A的位置为A′,并且平面A′BD⊥平面BCD.给出下面四个命题:
如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起.设折起后点A的位置为A′,并且平面A′BD⊥平面BCD.给出下面四个命题:①A′D⊥BC;
②三棱锥A′-BCD的体积为
| ||
| 2 |
③CD⊥平面A′BD;
④平面A′BC⊥平面A′DC.
其中正确命题的序号是( )
| A、①② | B、③④ | C、①③ | D、②④ |
考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:由题意证出BD⊥DC,然后结合平面PBD⊥平面BCD利用线面垂直的性质定理得CD⊥平面PBD,从而可判断①③;
三棱锥A′-BCD的体积为
•
•
•
•
=
,可判断②;
利用折叠前四边形ABCD中的性质与数量关系,可证BD⊥CD,再利用折叠后BCD平面PBD⊥平面,可证CD⊥平面PBD,从而证明CD⊥PB,再证明PB⊥平面PDC,然后利用线面垂直证明面面垂直.
三棱锥A′-BCD的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 6 |
利用折叠前四边形ABCD中的性质与数量关系,可证BD⊥CD,再利用折叠后BCD平面PBD⊥平面,可证CD⊥平面PBD,从而证明CD⊥PB,再证明PB⊥平面PDC,然后利用线面垂直证明面面垂直.
解答:
解:①∵∠BAD=90°,AD=AB,
∴∠ADB=∠ABD=45°,
∵AD∥BC,∠BCD=45°,
∴BD⊥DC,
∵平面A′BD⊥平面BCD,CD?平面BCD,
∴CD⊥平面A′BD,
∵A′D?平面A′BD,
∴CD⊥A′D,故A′D⊥BC不成立;故①错误;
②三棱锥A′-BCD的体积为
•
•
•
•
=
,故②不成立;
③由①知CD⊥平面A′BD,故③成立;
④折叠前,在四边形ABCD中,AD∥BC,AD=AB,∠BAD=90°,
∴△ABD为等腰直角三角形.
又∵∠BCD=45°,∠DBC=45°,
∴∠BDC=90°.
折叠后,∵平面BCD⊥平面A′BD,CD⊥BD,
∴CD⊥平面A′BD.
又∵A′B?平面A′BD,
∴CD⊥A′B.
又A′B⊥A′D,A′D∩CD=D,
∴A′B⊥平面A′DC.又A′B?平面A′BC,
∴平面A′BC⊥平面A′DC.故④正确.
故选:B.
∴∠ADB=∠ABD=45°,
∵AD∥BC,∠BCD=45°,
∴BD⊥DC,
∵平面A′BD⊥平面BCD,CD?平面BCD,
∴CD⊥平面A′BD,
∵A′D?平面A′BD,
∴CD⊥A′D,故A′D⊥BC不成立;故①错误;
②三棱锥A′-BCD的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 6 |
③由①知CD⊥平面A′BD,故③成立;
④折叠前,在四边形ABCD中,AD∥BC,AD=AB,∠BAD=90°,
∴△ABD为等腰直角三角形.
又∵∠BCD=45°,∠DBC=45°,
∴∠BDC=90°.
折叠后,∵平面BCD⊥平面A′BD,CD⊥BD,
∴CD⊥平面A′BD.
又∵A′B?平面A′BD,
∴CD⊥A′B.
又A′B⊥A′D,A′D∩CD=D,
∴A′B⊥平面A′DC.又A′B?平面A′BC,
∴平面A′BC⊥平面A′DC.故④正确.
故选:B.
点评:本题通过折叠性问题,考查了面面垂直的性质,面面垂直的判定,考查了体积的计算,关键是利用好直线与平面,平面与平面垂直关系的转化.

练习册系列答案
相关题目
下列方程中(t为参数)与方程y2=x表示同一曲线的是( )
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|
已知数列{an}满足3an+1+an=0,a2=-
,则a10等于( )
| 4 |
| 3 |
| A、-4×3-9 |
| B、4×3-9 |
| C、-4×37 |
| D、4×37 |
若关于x的不等式ax2-(a+1)x+1<0(a∈R)的解集为(
,1),则a的取值范围为( )
| 1 |
| a |
| A、a<0,或a>1 | B、a>1 |
| C、0<a<1 | D、a<0 |
直线3x+4y+11=0与圆(x-1)2+(y+1)2=1的位置关系为( )
| A、过圆心 | B、相离 | C、相切 | D、相交 |
函数f(x)=max{x2-x,1-x2}的单调增区间是( )
A、[-
| ||
B、(-∞,-
| ||
C、[-
| ||
| D、[0,1] |
若曲线y=
,与直线y=kx-1有两个不同的交点,则实数k的取值范围是( )
|
A、(3-2
| ||||
B、(0,3-2
| ||||
C、(-∞,0)∪(0,3-2
| ||||
D、(-∞,3-2
|
 如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,E是PC的三等分点,F是PB的中点,求证:AF∥面BDE.
如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,E是PC的三等分点,F是PB的中点,求证:AF∥面BDE.