题目内容
已知a、b是两个不相等的正数，且满足a3-b3=a2-b2，求所有可能的整数c，使c=9a•b．
考点：进行简单的合情推理
专题：函数的性质及应用
分析：根据题意及立方差公式的展开形式可得出a2+ab+b2=a+b的值，然后可求出ab与a+b的关系式，结合基本不等式即可得出答案．
解答：
解：∵a3-b3=a2-b2，
∴（a-b）（a2+ab+b2）=（a-b）（a+b）
∵a，b为不相等的两正数
∴a2+ab+b2=a+b，
∴（a+b）2-（a+b）=ab，
又0＜ab＜
，
∴0＜（a+b）2-（a+b）＜
，
解得，1＜a+b＜
，
令t=a+b，则（a+b）2-（a+b）=t2-t．
∵y=t2-t的图象是开口朝上，且以直线t=
为对称轴的抛物线，
故y=t2-t在（1，
）上递增，
故t2-t∈（0，
），
即ab=（a+b）2-（a+b）∈（0，
），
∴c=9a•b∈（0，4），
故满足条件的整数c∈{1，2，3}
∴（a-b）（a2+ab+b2）=（a-b）（a+b）
∵a，b为不相等的两正数
∴a2+ab+b2=a+b，
∴（a+b）2-（a+b）=ab，
又0＜ab＜
| (a+b)2 |
| 4 |
∴0＜（a+b）2-（a+b）＜
| (a+b)2 |
| 4 |
解得，1＜a+b＜
| 4 |
| 3 |
令t=a+b，则（a+b）2-（a+b）=t2-t．
∵y=t2-t的图象是开口朝上，且以直线t=
| 1 |
| 2 |
故y=t2-t在（1，
| 4 |
| 3 |
故t2-t∈（0，
| 4 |
| 9 |
即ab=（a+b）2-（a+b）∈（0，
| 4 |
| 9 |
∴c=9a•b∈（0，4），
故满足条件的整数c∈{1，2，3}
点评：本题考查基本不等式、立方公式的应用，难度不大，注意掌握立方公式的特点结合完全平方式是解答本题的关键．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
若关于x的不等式ax2-（a+1）x+1＜0（a∈R）的解集为（
，1），则a的取值范围为（ ）
| 1 |
| a |
| A、a＜0，或a＞1 | B、a＞1 |
| C、0＜a＜1 | D、a＜0 |
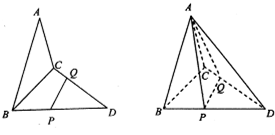如图，已知三角形△ABC与△BCD所在平面相互垂直，且∠BAC=∠BCD=90°，AB=AC，CB=CD，点P，Q分别在线段BD，CD上，沿直线PQ将△PQD向上翻折，使D与A重合．
如图，椭圆C：
如图，在四棱锥P-ABCD中，四边形ABCD是平行四边形，E是PC的三等分点，F是PB的中点，求证：AF∥面BDE．