题目内容
在等差数列{an}中，已知a2+a10=16，则a4+a8=（ ）
| A、12 | B、16 | C、20 | D、24 |
考点：等差数列的性质
专题：等差数列与等比数列
分析：直接利用等差数列的性质得答案．
解答：
解：∵数列{an}是等差数列，且a2+a10=16，
∴由等差数列的性质，得a4+a8=a2+a10=16．
故选：B．
∴由等差数列的性质，得a4+a8=a2+a10=16．
故选：B．
点评：本题考查了等差数列的性质，在等差数列中，若m，n，p，q∈N*，且m+n=p+q，则am+an=ap+aq，是基础题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
下列式子中成立的是（ ）
A、log
| ||||
B、（
| ||||
C、（
| ||||
| D、log32＞log23 |
过点（
，
）且被圆C：x2+y2-2x-4y=0截得的最短弦的弦长为（ ）
| 5 |
| 2 |
| 3 |
| 2 |
A、3
| ||
B、
| ||
C、
| ||
D、
|
若a，b∈R，且ab＞0，则下列不等式中，恒成立的是（ ）
| A、a2+b2＞2ab | ||
B、a+b≥2
| ||
C、a+b＞2
| ||
| D、a2+b2≥2ab |
若关于x的不等式ax2-（a+1）x+1＜0（a∈R）的解集为（
，1），则a的取值范围为（ ）
| 1 |
| a |
| A、a＜0，或a＞1 | B、a＞1 |
| C、0＜a＜1 | D、a＜0 |
已知f（x）=ax3+2x2+1，若f′（-1）=4，则a=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=max{x2-x，1-x2}的单调增区间是（ ）
A、[-
| ||
B、（-∞，-
| ||
C、[-
| ||
| D、[0，1] |
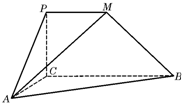如图，PCBM是直角梯形，∠PCB=90°，PM∥BC，PM=1，BC=2，又AC=1，∠ACB=120°，AB⊥PC，直线AM与直线PC所成的角为60°．