题目内容
圆锥的底面半径为1，侧面展开图是一个半圆，则此圆锥的表面积为（ ）
| A、6π | ||||
| B、5π | ||||
| C、3π | ||||
D、
|
考点：旋转体（圆柱、圆锥、圆台）
专题：计算题,空间位置关系与距离
分析：利用圆锥侧面展开图的弧长=底面周长，可求得圆锥的底面周长以及圆锥母线长，那么圆锥的侧面积=底面周长×母线长÷2，即可求出圆锥的表面积．
解答：
解：底面半径为1，则底面周长=2π，侧面展开图是半圆，则母线长=2π×2÷2π=2，
∴圆锥的侧面积=
×2π×2=2π．
∵圆锥的底面积为π，
∴圆锥的表面积为2π+π=3π
故选C．
∴圆锥的侧面积=
| 1 |
| 2 |
∵圆锥的底面积为π，
∴圆锥的表面积为2π+π=3π
故选C．
点评：本题利用了圆的周长公式和扇形面积公式求解．牢记圆锥与扇形各个元素之间的关系是解决此类题目的关键．
练习册系列答案
阅读快车系列答案
相关题目
设数列{an}是首项为1，公比为q（q≠-1）的等比数列，若{
}是等差数列，则（
+
）+（
+
）+…+（
+
）=（ ）
| 1 |
| an+an+1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a2013 |
| 1 |
| a2014 |
| A、2012 | B、2013 |
| C、4024 | D、4026 |
若关于x的不等式ax2-（a+1）x+1＜0（a∈R）的解集为（
，1），则a的取值范围为（ ）
| 1 |
| a |
| A、a＜0，或a＞1 | B、a＞1 |
| C、0＜a＜1 | D、a＜0 |
函数f（x）=max{x2-x，1-x2}的单调增区间是（ ）
A、[-
| ||
B、（-∞，-
| ||
C、[-
| ||
| D、[0，1] |
若曲线y=
，与直线y=kx-1有两个不同的交点，则实数k的取值范围是（ ）
|
A、（3-2
| ||||
B、（0，3-2
| ||||
C、（-∞，0）∪（0，3-2
| ||||
D、（-∞，3-2
|
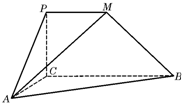如图，PCBM是直角梯形，∠PCB=90°，PM∥BC，PM=1，BC=2，又AC=1，∠ACB=120°，AB⊥PC，直线AM与直线PC所成的角为60°．
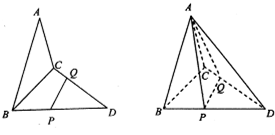如图，已知三角形△ABC与△BCD所在平面相互垂直，且∠BAC=∠BCD=90°，AB=AC，CB=CD，点P，Q分别在线段BD，CD上，沿直线PQ将△PQD向上翻折，使D与A重合．