题目内容
已知曲线C1的参数方程为
(t为参数),当t=1时,曲线C1上的点为A,当t=-1时,曲线C1上的点为B.以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=
.
(1)求A、B的极坐标;
(2)设M是曲线C2上的动点,求|MA|2+|MB|2的最大值.
|
| 6 | ||
|
(1)求A、B的极坐标;
(2)设M是曲线C2上的动点,求|MA|2+|MB|2的最大值.
考点:参数方程化成普通方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(1)当t=1时,代入参数方程可得即A(-1,
),利用ρ=
,tanθ=
即可得出
点A的极坐标,同理可得B(1,-
)及其点B的极坐标.
(2)由ρ=
,化为4ρ2+5(ρsinθ)2=36,利用
即可化为直角坐标方程,设曲线C2上的动点M(3cosα,2sinα),可得|MA|2+|MB|2=10cos2α+16,再利用余弦函数的单调性即可得出.
| 3 |
| x2+y2 |
| y |
| x |
点A的极坐标,同理可得B(1,-
| 3 |
(2)由ρ=
| 6 | ||
|
|
解答:
解:(1)当t=1时,代入参数方程可得
即A(-1,
),
∴ρ=
=2,tanθ=
=-
,∴θ=
,∴点A的极坐标为(2,
).
当t=-1时,同理可得B(1,-
),点B的极坐标为(2,
).
(2)由ρ=
,化为ρ2(4+5sin2θ)=36,∴4ρ2+5(ρsinθ)2=36,化为4(x2+y2)+5y2=36,化为
+
=1,设曲线C2上的动点M(3cosα,2sinα),
则|MA|2+|MB|2=(3cosα+1)2+(2sinα-
)2+(3cosα-1)2+(2sinα+
)2
=18cos2α+8sin2α+8
=10cos2α+16≤26,当cosα=±1时,取得最大值26.
∴|MA|2+|MB|2的最大值是26.
|
| 3 |
∴ρ=
(-1)2+(
|
| ||
| -1 |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
当t=-1时,同理可得B(1,-
| 3 |
| 5π |
| 3 |
(2)由ρ=
| 6 | ||
|
| x2 |
| 9 |
| y2 |
| 4 |
则|MA|2+|MB|2=(3cosα+1)2+(2sinα-
| 3 |
| 3 |
=18cos2α+8sin2α+8
=10cos2α+16≤26,当cosα=±1时,取得最大值26.
∴|MA|2+|MB|2的最大值是26.
点评:本题考查了把极坐标方程化为直角坐标方程、椭圆的标准方程及其参数方程、三角函数基本关系式、余弦函数的单调性等基础知识与基本技能方法,考查了计算能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
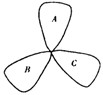 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是( )
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是( )