题目内容
若A为不等式组
表示的平面区域,则A的面积为 ;当a的值从-2连续变化到1时,动直线l:x+y=a扫过的A中的那部分区域的面积为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,即可求出A的面积.
解答:
解:不等式组对应的平面区域如图: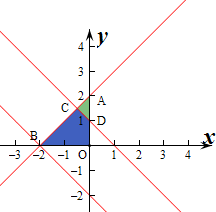
则不等式组对应的区域为直角三角形OAB,对应的面积为
×2×2=2,
当a的值从-2连续变化到1时,动直线l:x+y=a扫过的A中的那部分区域为四边形OBCD,
由
得
,即C(-
,
),
B(-2,0),D(0,1),
则四边形OBCD的面积S=S△OAB-S△ACD=2-
×(2-1)×
=2-
=
.
故答案为:2,
.

则不等式组对应的区域为直角三角形OAB,对应的面积为
| 1 |
| 2 |
当a的值从-2连续变化到1时,动直线l:x+y=a扫过的A中的那部分区域为四边形OBCD,
由
|
|
| 1 |
| 2 |
| 3 |
| 2 |
B(-2,0),D(0,1),
则四边形OBCD的面积S=S△OAB-S△ACD=2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 7 |
| 4 |
故答案为:2,
| 7 |
| 4 |
点评:本题主要考查二元一次不等式组表示平面,根据对应区域即可求出相应的面积.

练习册系列答案
相关题目
已知集合U=R,集合A={x|-l≤x≤3},集合B=|x|log2x<2},则A∩B=( )
| A、{x|1≤x≤3} |
| B、{x|-1≤x≤3} |
| C、{x|0<x≤3} |
| D、{x|-1≤x<0} |
如图给出的是计算
+
+
+…+
的值的一个程序框图,则判断框内应填入的条件是( )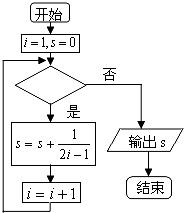
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2013 |

| A、i≥2013? |
| B、i≤1007? |
| C、i<2013? |
| D、i>1007? |
 有一个奇数组成的数阵排列如图:则第30行从左到右第3个数是
有一个奇数组成的数阵排列如图:则第30行从左到右第3个数是