题目内容
给出四个命题：
①“f（0）=0”是“函数f（x）是奇函数”的充要条件
②“向量
，
，
，若
•
=
•
，则
=
”是真命题
③“对任意的x∈R，x2+1＞0”的否定是“存在x0∈R，
+1＜0”
④“若α=
，则sinα=
”的否命题是“α≠
，则sinα≠
”
说法正确的个数是（ ）
①“f（0）=0”是“函数f（x）是奇函数”的充要条件
②“向量
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
③“对任意的x∈R，x2+1＞0”的否定是“存在x0∈R，
| x | 2 0 |
④“若α=
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
说法正确的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：命题的真假判断与应用
专题：综合题,简易逻辑
分析：①函数值等于0，不能判定函数的奇偶性，函数是一个奇函数也不一定使得在x=0处的函数值等于0，有的函数在x=0处没有意义，故前者不能推出后者，后者也不能推出前者；
②向量的数量积运算，不满足消去率；
③“对任意的x∈R，x2+1＞0”的否定是“存在x0∈R，
+1≤0”；
④若p则q的否命题是：若￢p则￢q．
②向量的数量积运算，不满足消去率；
③“对任意的x∈R，x2+1＞0”的否定是“存在x0∈R，
| x | 2 0 |
④若p则q的否命题是：若￢p则￢q．
解答：
解：①函数值等于0，不能判定函数的奇偶性，函数是一个奇函数也不一定使得在x=0处的函数值等于0，有的函数在x=0处没有意义，故前者不能推出后者，后者也不能推出前者，故①不正确；
②向量的数量积运算，不满足消去率，故“向量
，
，
，若
•
=
•
，则
=
”是假命题，即②不正确；
③“对任意的x∈R，x2+1＞0”的否定是“存在x0∈R，
+1≤0”，故③不正确；
④“若α=
，则sinα=
”的否命题是“α≠
，则sinα≠
”，正确．
故选：B．
②向量的数量积运算，不满足消去率，故“向量
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
③“对任意的x∈R，x2+1＞0”的否定是“存在x0∈R，
| x | 2 0 |
④“若α=
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
故选：B．
点评：本题主要考查各种命题的真假判断，考查学生分析解决问题的能力，综合性较强．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
下列命题中正确的是（ ）
| A、20.3＞1＞0.32 | ||||
| B、?m，n∈R+，lg（m+n）=lgm•lgn | ||||
C、0.31
| ||||
D、如果a
|
如图给出的是计算
+
+
+…+
的值的一个程序框图，则判断框内应填入的条件是（ ）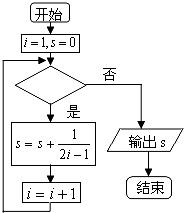
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2013 |
| A、i≥2013？ |
| B、i≤1007？ |
| C、i＜2013？ |
| D、i＞1007？ |
如图程序输出的结果是（ ）
| A、3 | B、7 | C、15 | D、19 |
已知点P（x，y）满足线性约束条件
，点M（3，1），O为坐标原点，则
•
的最大值为（ ）
|
| OM |
| OP |
| A、12 | B、11 | C、3 | D、-1 |
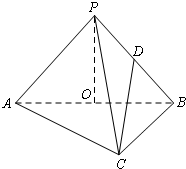如图，三棱锥P-ABC中，已知平面PAB⊥平面ABC，AC⊥BC，AC=BC=2a，点O，D分别是AB，PB的中点，PO⊥AB，连结CD．