题目内容
设a，b∈R，比较a2+3b2与b（2b-a）的大小，并说明理由．
考点：不等式比较大小
专题：不等式的解法及应用
分析：利用“作差法”和“配方法”即可比较出大小．
解答：
解：a2+3b2-b（2b-a）=a2+ab+b2=(a+
b)2+
b2≥0，当且仅当a=b=0时取等号．
∴a2+3b2≥b（2b-a）．
| 1 |
| 2 |
| 3 |
| 4 |
∴a2+3b2≥b（2b-a）．
点评：本题考查了“作差法”和“配方法”比较两个数的大小，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
设y=x4+ln3，则y′=（ ）
| A、4x3 | ||
B、4x3+
| ||
| C、x4lnx | ||
D、x4lnx+
|
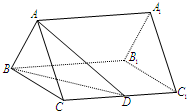如图，已知正三棱柱ABC-A1B1C1的底面边长是2，D是侧棱CC1的中点，直线AD与侧面BB1C1C所成的角为45°．