题目内容
设全集U=R，已知集合A={x|x≥1}，B={x|（x+2）（x-1）＜0}，则（ ）
| A、A∪B=U |
| B、A∩B=∅ |
| C、∁UB⊆A |
| D、∁UA⊆B |
考点：交集及其运算,一元二次不等式的解法
专题：集合
分析：求出B中不等式的解集确定出B，求出A与B的并集，交集，以及A与B的补集，即可做出判断．
解答：
解：由B中的不等式解得：-2＜x＜1，即B={x|-2＜x＜1}，
∵A={x|x≥1}，全集U=R，
∴A∪B={x|x＞-2}；A∩B=∅；∁UB={x|x≤-2或x≥1}；∁UA={x|x＜1}，
故选：B．
∵A={x|x≥1}，全集U=R，
∴A∪B={x|x＞-2}；A∩B=∅；∁UB={x|x≤-2或x≥1}；∁UA={x|x＜1}，
故选：B．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
函数f（x）的定义域为D，满足：①f（x）在D内是单调函数；②存在[
，
]⊆D，使得f（x）在[
，
]上的值域为[a，b]，那么就称函数y=f（x）为“优美函数”，若函数f（x）=logc（cx-t）（c＞0，c≠1）是“优美函数”，则t的取值范围为（ ）
| a |
| 2 |
| b |
| 2 |
| a |
| 2 |
| b |
| 2 |
| A、（0，1） | ||
B、（0，
| ||
C、（-∞，
| ||
D、（0，
|
椭圆
+
=1的焦距为2，则m的取值是（ ）
| x2 |
| m |
| y2 |
| 6 |
| A、7 | B、5 | C、5或7 | D、10 |
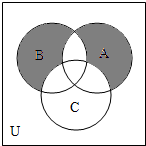如图所示，已知集合A、B、C为全集U的子集，则图中阴影部分所表示的集合为（ ）| A、（∁∪C）∪（A∪B） |
| B、（A∪B）∩[∁∪（A∩B）] |
| C、（A∪B）∩[∁∪（A∩B∩C）] |
| D、{A∩[∁∪（B∪C）]}∪{B∩[∁∪（A∪C）]} |
已知变量x，y满足条件：
，则z=
的取值范围（ ）
|
| y |
| x |
| A、[1，2] | ||||
B、[1，
| ||||
C、[-1，
| ||||
D、[
|
已知x，y满足约束条件
，那么z=2x+3y的最小值为（ ）
|
A、
| ||
| B、8 | ||
C、
| ||
| D、10 |