题目内容
在平面直角坐标系中有两点A（-1，3
）、B（1，
），以原点为圆心，r＞0为半径作一个圆，与射线y=-
x（x＜0）交于点M，与x轴正半轴交于N，则当r变化时，|AM|+|BN|的最小值为 ．
| 3 |
| 3 |
| 3 |
考点：两点间距离公式的应用
专题：计算题,转化思想,推理和证明
分析：由题意，设M（a，-
a）（a＜0），则r=-2a，N（-2a，0）．可得|AM|+|BN|=
+
，设2a=x，进而可以理解为（x，0）与（-
，
）和（-1，
）的距离和，即可得出结论．
| 3 |
(a+1)2+(-
|
| (2a+1)2+3 |
| 5 |
| 3 |
| 3 |
解答：
解：由题意，设M（a，-
a）（a＜0），则r=-2a，N（-2a，0）．
∴|AM|+|BN|=
+
设2a=x，则|AM|+|BN|=
+
，
可以理解为（x，0）与（-5，
）和（-1，
）的距离和，
∴|AM|+|BN|的最小值为（-5，
）和（-1，-
）的距离，即2
．
故答案为：2
．
| 3 |
∴|AM|+|BN|=
(a+1)2+(-
|
| (2a+1)2+3 |
设2a=x，则|AM|+|BN|=
(x+5)2+(0-
|
(x+1)2+(0-
|
可以理解为（x，0）与（-5，
| 3 |
| 3 |
∴|AM|+|BN|的最小值为（-5，
| 3 |
| 3 |
| 7 |
故答案为：2
| 7 |
点评：本题考查两点间距离公式的应用，考查学生分析解决问题的能力，有难度．
练习册系列答案
相关题目
△ABC的外接圆的圆心为O，若
=
+
+
，则H是△ABC的（ ）
| OH |
| OA |
| OB |
| OC |
| A、外心 | B、内心 | C、重心 | D、垂心 |
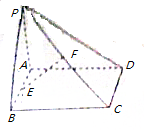已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB、PC的中点．
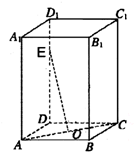如图，在长方体ABCD-A1B1C1D1中，O为AC的中点，设E是棱DD1上的点，且