题目内容

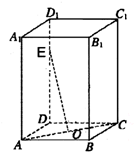如图，在长方体ABCD-A1B1C1D1中，O为AC的中点，设E是棱DD1上的点，且
DE
=
2
3
DD1
，若
EO
=x
AB
+y
AD
+z
AA1
，则x+y+z的值为（　　）
A、
5
6
B、-
5
6
C、-
2
3
D、
4
5
考点：平面向量的基本定理及其意义
专题：空间向量及应用
分析：
EO
=
ED
+
DO
，
DE
=
2
3
DD1
=
2
3
AA1
，
DO
=
1
2
DB
=
1
2
(
AB
-
AD
)，化简整理可得
EO
=-
2
3
AA1
+
1
2
AB
-
1
2
AD
，与
EO
=x
AB
+y
AD
+z
AA1
比较即可得出．
解答： 解：∵
EO
=
ED
+
DO
，
DE
=
2
3
DD1
=
2
3
AA1
，
DO
=
1
2
DB
=
1
2
(
AB
-
AD
)，
∴
EO
=-
2
3
AA1
+
1
2
AB
-
1
2
AD
，
与
EO
=x
AB
+y
AD
+z
AA1
，
∴x=
1
2
，y=-
1
2
，z=-
2
3
．
∴x+y+z=-
2
3
．
故选：C．
点评：本题考查了向量的三角形法则、空间向量基本定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
在平面直角坐标系中有两点A（-1，3
3
）、B（1，
3
），以原点为圆心，r＞0为半径作一个圆，与射线y=-
3
x（x＜0）交于点M，与x轴正半轴交于N，则当r变化时，|AM|+|BN|的最小值为
 
．
对于△ABC，总满足：
CD
=sin2θ
CA
+cos2θ
CB
，
CD
•
AB
=
3
|AB|2，且
1
tan∠A
-
1
tan∠B
-
2
tan∠BDC
=1恒成立，则：
①△ABC一定是钝角三角形；②CA＜CB；③?x∈R，θ=x；
④∠ADC的最小值小于30°；⑤CD可能是一条中线；⑥∠C的最大值小于30°．
上述对于△ABC的描述错误的是：
 
．
已知数列{an}满足a1=1，an+1=an+n+2n（n∈N*），则an等于（　　）
A、
n(n-1)
2
+2n-1-1
B、
n(n-1)
2
+2n-1
C、
n(n+1)
2
+2n+1-1
D、
n(n-1)
2
+2n+1-1
在梯形中ABCD，AB∥CD，AB=2CD，M，N分别是CD，AB的中点，设
AB
=
e1
，
AD
=
e2
．
（1）在图上作出向量
1
2
e1
+
e2
（不要求写出作法）
（2）请将
MN
用
e1
，
e2
表示．
已知P是圆F1：（x+1）2+y2=8上任意一点，又F2（1，0），直线m分别与线段F1P，F2P交于M，N两点，且
MN
=
1
2
（
MF2
+
MP
），|
NM
+
F2P
|=|
NM
-
F2P
|．
（1）求点M的轨迹C的方程；
（2）直线x=my+2与椭圆交于A、B两点，点D在椭圆上，且
OA
+
OB
=λ
OD
，E（-
2
m
，
m-2
m
），设△EAB的面积为S，若0＜S≤1，求λ的取值范围．
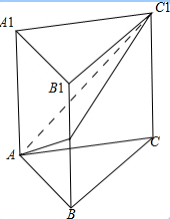如图，直三棱柱ABC-A1B1C中，AB⊥BC，AB=4，BC=6，AA1=8，有一只蚂蚁沿着三棱柱的表面从点A爬行到点C1，并且在棱BB1上的一点M稍作停顿，当蚂蚁爬行距离最短时，BM的长度为
 
．
已知圆C与直线l：x+y-2=0和圆P：（x-6）2+（y-6）2=18均相切，求圆C的面积的最小值及此时圆C的方程．
已知sin（2α+
5π
6
）=
1
3
，α∈（0，
π
3
），则sin2α=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网