题目内容
已知在三棱锥O-ABC中,OA=OB=OC=1,∠AOB=60°,∠AOC=∠BOC=90°,G是△ABC的重心,求直线OG与BC所成角的余弦值.
考点:异面直线及其所成的角
专题:空间角
分析:以O为原点,OA为y轴,OC为z轴,建立空间直角坐标系,利用向量法能求出直线OG与BC所成角的余弦值.
解答:
解:以O为原点,OA为y轴,OC为z轴,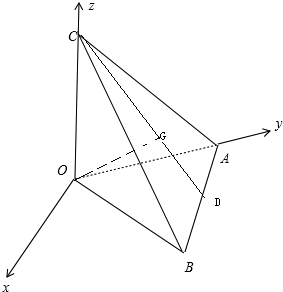
建立空间直角坐标系,
由已知得A(0,1,0),B(
,
,0),
设D为AB中点,则D(
,
,0),
C(0,0,1),设G(a,b,c),
∵G是△ABC的重心,∴
=
,
∴(a,b,c-1)=
(
,
,-1)=(
,
,-
),
∴a=
,b=
,c=
,∴G(
,
,
),
∴
=(
,
,-1),
=(
,
,
),
设直线OG与BC所成角为θ,
∴cosθ=
=
.
∴直线OG与BC所成角的余弦值为
.

建立空间直角坐标系,
由已知得A(0,1,0),B(
| ||
| 2 |
| 1 |
| 2 |
设D为AB中点,则D(
| ||
| 4 |
| 3 |
| 4 |
C(0,0,1),设G(a,b,c),
∵G是△ABC的重心,∴
| CG |
| 2 |
| 3 |
| CD |
∴(a,b,c-1)=
| 2 |
| 3 |
| ||
| 4 |
| 3 |
| 4 |
| ||
| 6 |
| 1 |
| 2 |
| 2 |
| 3 |
∴a=
| ||
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
∴
| CB |
| ||
| 2 |
| 1 |
| 2 |
| OG |
| ||
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
设直线OG与BC所成角为θ,
∴cosθ=
|
| ||||
|
|
| ||
| 8 |
∴直线OG与BC所成角的余弦值为
| ||
| 8 |
点评:本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
若A、B两点的坐标分别是A(3cosa,3sina,1),B(2cosb,2sinb,1),则|
|的取值范围是( )
| AB |
| A、[0,5] |
| B、[1,5] |
| C、(1,5) |
| D、[1,25] |
已知数列{an}满足a1=1,an+1=an+n+2n(n∈N*),则an等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
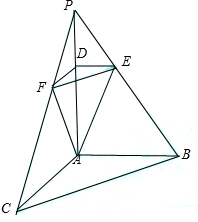 在三棱椎P-ABC中,PA⊥平面ABC,AC=AB=
在三棱椎P-ABC中,PA⊥平面ABC,AC=AB=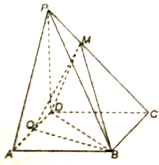 如图,在四棱锥P-ABCD中,底面ABCD为菱形,PD⊥平面ABCD,∠BAD=60°,Q为AD中点,AD=4,PD=6.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,PD⊥平面ABCD,∠BAD=60°,Q为AD中点,AD=4,PD=6.