题目内容
下列三数
,log1682,log27124的大小关系是( )
| 3 |
| 2 |
A、
| ||
B、
| ||
C、log27124<
| ||
D、log27124<log1682<
|
考点:对数值大小的比较
专题:综合题
分析:利用对数的运算性质,分别把
与log1682,
与log27124化为同底数的对数,通过比较真数的大小得结论.
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:∵log27124=log33124=
log3124=log3
=log3
=log3
.
=
log33=log3
=log3
=log3
.
∵19683>15376,
∴log27124<
.
又log1682=log2482=
log282=log2
=
log2
=log2
.
∵64<82,∴
<log1682.
∴三数
,log1682,log27124的大小关系是log27124<
<log1682.
故选:C.
| 1 |
| 3 |
| 3 | 124 |
| 6 | 1242 |
| 6 | 15376 |
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 6 | 273 |
| 6 | 19683 |
∵19683>15376,
∴log27124<
| 3 |
| 2 |
又log1682=log2482=
| 1 |
| 4 |
| 4 | 82 |
| 3 |
| 2 |
| 3 |
| 2 |
| 8 |
| 4 | 64 |
∵64<82,∴
| 3 |
| 2 |
∴三数
| 3 |
| 2 |
| 3 |
| 2 |
故选:C.
点评:本题考查了对数值的大小比较,解答的关键是化为同底数的对数,属中档题.

练习册系列答案
相关题目
函数y=3x+1(x≥-1)的值域是( )
| A、(0,+∞) |
| B、(1,+∞) |
| C、[0.+∞) |
| D、[1.+∞) |
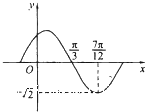 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则Atanφ的值为( )
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则Atanφ的值为( )A、-
| ||
B、-
| ||
C、
| ||
D、
|
要得到函数y=cos3x的图象,只需将函数y=sin3x的图象( )
A、右移
| ||
B、左移
| ||
C、右移
| ||
D、左移
|
已知椭圆
+y2=1(m>1)和双曲线
-y2=1(n>0)有相同的焦点F1,F2,P是它们的一个交点,则△F1PF2的形状是( )
| x2 |
| m |
| x2 |
| n |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、随m,n的变化而变化 |
已知点(a,b)是直线x+y=2在第一象限内的一个动点,则z=
+
的最小值是( )
| 1 |
| a |
| 4 |
| b |
A、
| ||
| B、4 | ||
C、
| ||
| D、9 |
设α﹑β为钝角,且sinα=
,cosβ=-
,则α+β的值为( )
| ||
| 5 |
3
| ||
| 10 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
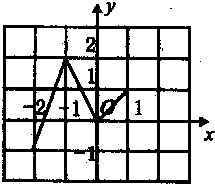 已知定义在R上的函数f(x)满足f(x)=f(x+3),如图表示 该函数在区间(-2,1]上的图象,则f(2011)+f(2012)等于( )
已知定义在R上的函数f(x)满足f(x)=f(x+3),如图表示 该函数在区间(-2,1]上的图象,则f(2011)+f(2012)等于( )