题目内容
过点P(2,1)的直线l与坐标轴分别交A,B两点,如果三角形OAB的面积为5,则满足条件的直线l最多有( )条.
| A、1 | B、2 | C、3 | D、4 |
考点:直线的截距式方程
专题:直线与圆
分析:设直线l的方程为:
+
=1,利用直线l过点P(2,1),得到
+
=1,再由△OAB的面积为5,得到
|a||b|=5,由此联立方程组能求出结果.
| x |
| a |
| y |
| b |
| 2 |
| a |
| 1 |
| b |
| 1 |
| 2 |
解答:
解:设直线l与坐标轴的交点A(a,0),B(0,b),
则直线l的方程为:
+
=1,
∵直线l过点P(2,1),∴
+
=1,①
∴△OAB的面积为5,
∴
|a||b|=5,②
联立①②,得
,
解得b=
,a=
,
∴满足条件的解有
,
,
,
;
∴直线l最多有4条,
故选:D.
则直线l的方程为:
| x |
| a |
| y |
| b |
∵直线l过点P(2,1),∴
| 2 |
| a |
| 1 |
| b |
∴△OAB的面积为5,
∴
| 1 |
| 2 |
联立①②,得
|
|
解得b=
5±
| ||
| 2 |
| 20 | ||
5±
|
∴满足条件的解有
|
|
|
|
∴直线l最多有4条,
故选:D.
点评:本题考查了满足条件的直线方程的求法,解题时要认真审题,注意直线的截距式方程的灵活运用.

练习册系列答案
相关题目
已知点O是以角B为直角顶点的△ABC的外心,且|
|=2,|
|=4,则
•
=( )
| AB |
| AC |
| AO |
| BC |
| A、2 | ||
| B、4 | ||
| C、6 | ||
D、2
|
cos210°等于( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
函数y=3x+1(x≥-1)的值域是( )
| A、(0,+∞) |
| B、(1,+∞) |
| C、[0.+∞) |
| D、[1.+∞) |
函数f(x)=π2x2的导数是( )
| A、f′(x)=4πx |
| B、f′(x)=2πx |
| C、f′(x)=2π2x |
| D、f′(x)=2πx2+2π2x |
执行如图的程序,若输出结果为2,则输入的实数x的值是( )


| A、3 | ||
B、
| ||
| C、4 | ||
| D、2 |
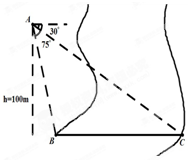 如图,在气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,若此时的气球高度是100m,则河流在B,C两地的宽度为
如图,在气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,若此时的气球高度是100m,则河流在B,C两地的宽度为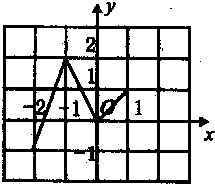 已知定义在R上的函数f(x)满足f(x)=f(x+3),如图表示 该函数在区间(-2,1]上的图象,则f(2011)+f(2012)等于( )
已知定义在R上的函数f(x)满足f(x)=f(x+3),如图表示 该函数在区间(-2,1]上的图象,则f(2011)+f(2012)等于( )