题目内容
若直线x+y=m与圆x2+y2=m相切,则m的值为( )
| A、0 | B、1 | C、2 | D、0或2 |
考点:圆的切线方程,直线与圆的位置关系
专题:计算题,直线与圆
分析:直线与圆相切,则圆心到直线的距离等于半径,从而可求得m的值.
解答:
解:圆x2+y2=m的圆心即为原点,
则圆心到直线x+y=m的距离,
d=
.
∵直线x+y=m与圆x2+y2=m相切,
∴d=r.
即
=
.
∴
=m.
∵m>0,
∴m=2.
故选C.
则圆心到直线x+y=m的距离,
d=
| |m| | ||
|
∵直线x+y=m与圆x2+y2=m相切,
∴d=r.
即
| |m| | ||
|
| m |
∴
| m2 |
| 2 |
∵m>0,
∴m=2.
故选C.
点评:本题考查直线与圆相切的性质,点到直线的距离公式等知识.属于中档题.

练习册系列答案
相关题目
执行如图的程序,若输出结果为2,则输入的实数x的值是( )


| A、3 | ||
B、
| ||
| C、4 | ||
| D、2 |
已知点(a,b)是直线x+y=2在第一象限内的一个动点,则z=
+
的最小值是( )
| 1 |
| a |
| 4 |
| b |
A、
| ||
| B、4 | ||
C、
| ||
| D、9 |
已知△ABC,角A、B、C所对应的边分别为a,b,c,且sinA+sinB=cosA+cosB,则△ABC是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰或直角三角形 |
设α﹑β为钝角,且sinα=
,cosβ=-
,则α+β的值为( )
| ||
| 5 |
3
| ||
| 10 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
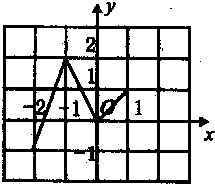 已知定义在R上的函数f(x)满足f(x)=f(x+3),如图表示 该函数在区间(-2,1]上的图象,则f(2011)+f(2012)等于( )
已知定义在R上的函数f(x)满足f(x)=f(x+3),如图表示 该函数在区间(-2,1]上的图象,则f(2011)+f(2012)等于( )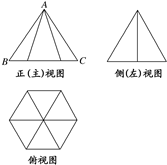 一个几何体的三视图如图所示,其中正(主)视图中△ABC是边长为2的正三角形,俯视图的边界为正六边形,那么该几何体的侧)视图的面积为( )
一个几何体的三视图如图所示,其中正(主)视图中△ABC是边长为2的正三角形,俯视图的边界为正六边形,那么该几何体的侧)视图的面积为( )