题目内容
函数f(x)=
+(x-1)0的定义域为( )
| 1 | ||
|
A、(-
| ||
| B、(-2,1)∪(1,+∞) | ||
C、(-
| ||
| D、(0,1)∪(1,+∞) |
考点:函数的定义域及其求法
专题:计算题,函数的性质及应用
分析:由分母中根式内部的代数式大于0,0指数幂的底数不等于0联立不等式组求解x的取值集合即可得到函数的定义域.
解答:
解:由
,得x>-
且x≠1.
∴函数f(x)=
+(x-1)0的定义域为(-
,1)∪(1,+∞).
故选:A.
|
| 1 |
| 2 |
∴函数f(x)=
| 1 | ||
|
| 1 |
| 2 |
故选:A.
点评:本题考查了函数的定义域及其求法,该题需要注意的是0指数幂的底数不等于0,是基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
cos210°等于( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知α是锐角,
=(
,sinα),
=(cosα,
),且
∥
,则α为( )
| a |
| 3 |
| 4 |
| b |
| 1 |
| 3 |
| a |
| b |
| A、15° | B、45° |
| C、75° | D、15°或75° |
已知三条直线a,b,c,若a和b是异面直线,b和c是异面直线,那么直线a和c的位置关系是( )
| A、平行 | B、相交 |
| C、异面 | D、平行、相交或异面 |
直线x+y=1与圆x2+y2=2的位置关系是( )
| A、相切 | B、相交 |
| C、相离 | D、不能确定 |
已知△ABC,角A、B、C所对应的边分别为a,b,c,且sinA+sinB=cosA+cosB,则△ABC是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰或直角三角形 |
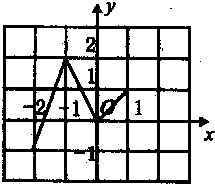 已知定义在R上的函数f(x)满足f(x)=f(x+3),如图表示 该函数在区间(-2,1]上的图象,则f(2011)+f(2012)等于( )
已知定义在R上的函数f(x)满足f(x)=f(x+3),如图表示 该函数在区间(-2,1]上的图象,则f(2011)+f(2012)等于( )