题目内容
4.柯西不等式是由数学家柯西在研究数学分析中的“流数”问题时得到的.具体表述如下:对任意实数a1,a2,…,an和b1,b2,…bn(n∈N+,n≥2),都有(a12+a22+…+an2)(b12+b22+…bn2)≥(a1b1+a2b2+…+anbn)2.(1)证明n=2时柯西不等式成立,并指出等号成立的条件;
(2)若对任意x∈[2,6],不等式3$\sqrt{x-2}$+2$\sqrt{6-x}$≤m恒成立,求实数m的取值范围(4分)
分析 (1)构造函数,利用判别式证明即可;
(2)利用柯西不等式求出(3$\sqrt{x-2}$+2$\sqrt{6-x}$)max,即可求实数m的取值范围.
解答 (1)证明:构造函数f(x)=(a1x+b1)2+(a2x+b2)2=(a12+a22)x2+2(a1b1+a2b2)x+(b12+b22).
注意到f(x)≥0,所以△=[2(a1b1+a2b2)]2-4(a12+a22)(b12+b22)≤0,
即(a1b1+a2b2)2≤(a12+a22)(b12+b22).
(其中等号成立当且仅当a1x+b1=a2x+b2=0,即a1b2=a2b1.)
(2)解:由(1)可得(3$\sqrt{x-2}$+2$\sqrt{6-x}$)2≤(32+22)[($\sqrt{x-2}$)2+($\sqrt{6-x}$)2]=52,
∴(3$\sqrt{x-2}$+2$\sqrt{6-x}$)max=2$\sqrt{13}$,
∵对任意x∈[2,6],不等式3$\sqrt{x-2}$+2$\sqrt{6-x}$≤m恒成立,
∴m≥$2\sqrt{13}$.
点评 本题是中档题,考查不等式的证明与应用,不等式求函数的最值,考查知识的应用能力,逻辑推理能力.

练习册系列答案
相关题目
14.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为45°,且|$\overrightarrow{a}$|=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2.则|$\overrightarrow{b}$|等于( )
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
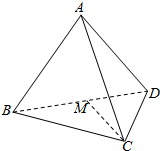 如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.
如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.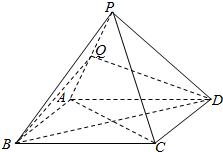 如图,四棱锥P-ABCD的底面ABCD为菱形,Q是棱PA的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,Q是棱PA的中点.