题目内容
9.若直线l与曲线y=x3相切于点P,且与直线y=3x+2平行,则点P的坐标为(1,1).分析 利用直线平行斜率相等求出切线的斜率,再利用导数在切点处的值是曲线的切线斜率求出切线斜率,列出方程解得即可.
解答 解:设切点P(m,m3),
由y=x3的导数为y′=3x2,
可得切线的斜率为k=3m2,
由切线与直线y=3x+2平行,
可得3m2=3,解得m=±1,
可得P(1,1),(-1,-1).
P(-1,-1)在直线y=3x+2上,舍去.
故答案为:(1,1).
点评 本题考查导数的几何意义:导数在切点处的值是切线的斜率,同时考查两直线平行的条件:斜率相等,属于基础题.

练习册系列答案
相关题目
19.设等差数列{an}的前n项和为Sn,其公差为-1,若S1,S2,S4成等比数列,则a1=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
18.如图,在长方体ABCD-A1B1C1D1中,AA1=2AB,AB=BC,则下列结论中正确的是( )
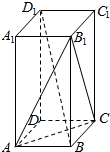

| A. | BD1∥B1C | B. | A1D1∥平面AB1C | C. | BD1⊥AC | D. | BD1⊥平面AB1C |
 如图,在直三棱柱ABC-A1B1C1中,已知A1C1⊥B1C1,CC1=2BC=2.
如图,在直三棱柱ABC-A1B1C1中,已知A1C1⊥B1C1,CC1=2BC=2.