题目内容
二项式(2
-
)5的展开式中含
项的系数为( )
| x |
| 1 |
| x |
| 1 |
| x2 |
| A、10 | B、-10 |
| C、40 | D、-40 |
考点:二项式系数的性质
专题:二项式定理
分析:先求出二项式展开式的通项公式,再令x的幂指数等于-2,求得r的值,即可求得展开式中含
项的系数.
| 1 |
| x2 |
解答:
解:二项式(2
-
)5的展开式的通项公式为 Tr+1=
•25-r•(-1)r•x
,
令
=-2,求得r=3,故展开式中含
项的系数为
•22•(-1)=-40,
故选:D.
| x |
| 1 |
| x |
| C | r 5 |
| 5-3r |
| 2 |
令
| 5-3r |
| 2 |
| 1 |
| x2 |
| C | 3 5 |
故选:D.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
4名男生和2名女生站成一排,则这2名女生不相邻的排法种数( )
| A、600 | B、480 |
| C、360 | D、120 |
若θ∈(
,2π),则
=( )
| 7π |
| 4 |
| 1-2sinθcosθ |
| A、cosθ-sinθ |
| B、sinθ+cosθ |
| C、sinθ-cosθ |
| D、-cosθ-sinθ |
已知数列{an}中,a3=2,a5=1,若{
}是等差数列,则a11等于( )
| 1 |
| 1+an |
| A、0 | ||
B、
| ||
C、
| ||
D、
|
已知点M在双曲线
-
=1上,它到左准线的距离为2,则它到左焦点的距离为( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、7 | ||
| B、3 | ||
C、
| ||
D、
|
在△ABC中,若c=acosB,则△ABC中一定为( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、锐角三角形 |
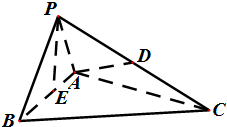 如图,四面体P-ABC中,△PAB为边长为1的等边三角形,△PBC与△PAC均为斜边为PC的直角三角形,且PC=
如图,四面体P-ABC中,△PAB为边长为1的等边三角形,△PBC与△PAC均为斜边为PC的直角三角形,且PC=