题目内容
在△ABC中，若c=acosB，则△ABC中一定为（ ）
| A、直角三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、锐角三角形 |
考点：正弦定理
专题：解三角形
分析：由条件利用正弦定理、诱导公式、两角和的正弦公式求得 cosAsinB=0，故有 cosA=0，求得 A=
，从而得出结论．
| π |
| 2 |
解答：
解：△ABC中，∵c=acosB，∴由正弦定理可得 sinC=sinAcosB，
∴sin（A+B）=sinAcosB+cosAsinB=sinAcosB，
∴cosAsinB=0，∴cosA=0，∴A=
，
故△ABC中一定为直角三角形，
故选：A．
∴sin（A+B）=sinAcosB+cosAsinB=sinAcosB，
∴cosAsinB=0，∴cosA=0，∴A=
| π |
| 2 |
故△ABC中一定为直角三角形，
故选：A．
点评：本题主要考查正弦定理、诱导公式、两角和的正弦公式的应用，属于中档题．
练习册系列答案
相关题目
王明早晨在6：30～7：00之间离开家去上学，送奶员在早上6：45～7：15之把牛奶送到王明家，则王明离开家之前能取到牛奶的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
阅读如图给出的程序框图，运行相应的程序，输出的结果S为（ ）
| A、-1007 | B、1007 |
| C、1008 | D、-3022 |
cos（-
π）的值为（ ）
| 79 |
| 6 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
二项式（2
-
）5的展开式中含
项的系数为（ ）
| x |
| 1 |
| x |
| 1 |
| x2 |
| A、10 | B、-10 |
| C、40 | D、-40 |
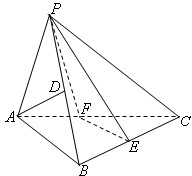在三棱锥P-ABC中，已知PA=PB，∠ABC为直角，点D，E分别为PB，BC的中点．