题目内容
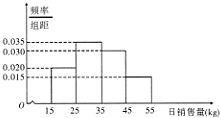根据市场统计，某商品的日销售量X（单位：kg）的频率分市直方图如图所示，则由频率分布直方图得到该商品日销售量的中位数的估计值为（ ）| A、35 | B、33.6 |
| C、30.7 | D、28.3 |
考点：频率分布直方图
专题：概率与统计
分析：由已知中的频率分布直方图，我们根据由直方图估算中位数的方法，我们可以计算出能把频率左右平均分成两半分成的x值，即可得到这些车辆速度的中位数的值．
解答：
解：由已知中，[15，25]的频率为0.020×10=0.2，
[15，35]的频率为（0.020+0.035）×10=0.55，
故该商品日销售量的中位数应在[25，35]之间
由于[25，35]的频率为0.35，
设该商品日销售量的中位数的值是x
则x=35-
=33.6．
故选：B．
[15，35]的频率为（0.020+0.035）×10=0.55，
故该商品日销售量的中位数应在[25，35]之间
由于[25，35]的频率为0.35，
设该商品日销售量的中位数的值是x
则x=35-
| 35-25 |
| 7 |
故选：B．
点评：本题考查的知识点是频率分面直方图，中位数，其中由频率分布直方图求中位数的步骤是：①先确定中位数在哪一段上；②根据比例的性质求出中位数．
练习册系列答案
相关题目
如图，一个三棱柱形容器中盛有水，且侧棱AA1=4，若侧面AA1B1B水平放置时，液面恰好过AC，BC，A1C1，B1C1的中点，当底面ABC水平放置时，液面的高为若四棱柱的侧面是全等的矩形，则该棱柱是（ ）
| A、长方体 | B、正四棱柱 |
| C、正方体 | D、底面是菱形的直棱柱 |
已知直线l过P（-m，6），Q（1，3m）两点，且l的倾斜角是直线l′：y=2x+1倾斜角的两倍，则实数m的值为（ ）
| A、-10 | ||
B、
| ||
C、
| ||
D、
|
在三棱锥A-BCD中，已知AB⊥平面BCD，∠BCD=90°，AB=a，BC=b，CD=c，a2+b2+c2=4，则三棱锥A-BCD的外接球的表面积为（ ）
A、
| ||
B、
| ||
| C、4π | ||
| D、16π |
规定甲乙两地通话m分钟的电话费由f（m）=1.06×（0.5×[m]+1）（单位：元）给出，其中m＞0，记[m]大于或等于m的最小整数（如：[4]=4，[3，8]=4），若从甲地到乙地通话费用为4.24元，则通话时间m的取值范围是（ ）
| A、（4，5] |
| B、（5，6] |
| C、（6，7] |
| D、（7，8] |
设m=x2+y2-2x+2y，n=-5，则m与n的大小关系是（ ）
| A、m＞n | B、m＜n |
| C、m=n | D、与x、y的取值有关 |
已知3x=log12（3y）+log12（
）（y＞0），则x的值是（ ）
| 4 |
| y |
| A、-1 | B、0 | C、1 | D、3 |