题目内容
设m=x2+y2-2x+2y，n=-5，则m与n的大小关系是（ ）
| A、m＞n | B、m＜n |
| C、m=n | D、与x、y的取值有关 |
考点：不等式的基本性质
专题：不等式的解法及应用
分析：利用“作差法”和配方法即可得出．
解答：
解：m-n=x2+y2-2x+2y+5=（x-1）2+（y-1）2+3≥3＞0，
∴m＞n．
故选：A．
∴m＞n．
故选：A．
点评：本题考查了“作差法”和配方法、实数的性质，属于基础题．
练习册系列答案
相关题目
设f（x）=lnx+2x-6，则下列区间中使f（x）=0有实数解的区间是（ ）
| A、[1，2] |
| B、[2，3] |
| C、[3，4] |
| D、[4，5] |
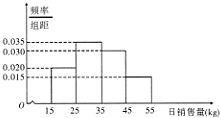根据市场统计，某商品的日销售量X（单位：kg）的频率分市直方图如图所示，则由频率分布直方图得到该商品日销售量的中位数的估计值为（ ）| A、35 | B、33.6 |
| C、30.7 | D、28.3 |
下列命题中错误的是（ ）
| A、如果平面α内的任何直线都平行平面β，则α∥β |
| B、如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β |
| C、如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么直线l⊥平面γ |
| D、如果平面α⊥平面β，α∩β=m，直线n⊥m，则n⊥β |
已知函数f（x）=x3+ax2+bx+a2在x=1处取极值10，则f（0）=（ ）
| A、9 | B、16 |
| C、9或16 | D、-9或16 |
已知⊙C的圆心C在y=
上，且⊙C过原点，OC交x轴、y轴于另两点A、B，则三角形OAB的面积为（ ）
| 1 |
| x |
| A、1 | B、2 | C、4 | D、8 |
点P（a，b）是⊙O：x2+y2=r2（r＞0）内一点，直线l1是以P为中点的弦所在直线，l2：ax+by=r2，则有（ ）
| A、l1⊥l2且l2与⊙O相离 |
| B、l1∥l2且l2与⊙O相离 |
| C、l1∥l2且l2与⊙O相交 |
| D、l1⊥l2且l2与⊙O相切 |
以线段AB：x+y-2=0（0≤x≤2）为直径的圆的方程为（ ）
| A、（x+1）2+（y+1）2=2 |
| B、（x-1）2+（y-1）2=2 |
| C、（x+1）2+（y+1）2=8 |
| D、（x-1）2+（y-1）2=8 |