题目内容
已知直线l过P(-m,6),Q(1,3m)两点,且l的倾斜角是直线l′:y=2x+1倾斜角的两倍,则实数m的值为( )
| A、-10 | ||
B、
| ||
C、
| ||
D、
|
考点:直线的斜率
专题:直线与圆
分析:设直线l′:y=2x+1倾斜角为θ,则tanθ=2.则l的倾斜角是2θ.则
=tan2θ,根据倍角公式即可得出.
| 6-3m |
| -m-1 |
解答:
解:设直线l′:y=2x+1倾斜角为θ,则tanθ=2.
则l的倾斜角是2θ.
∴
=tan2θ=
=
,解得m=
.
故选:B.
则l的倾斜角是2θ.
∴
| 6-3m |
| -m-1 |
| 2tanθ |
| 1-tan2θ |
| 2×2 |
| 1-22 |
| 14 |
| 13 |
故选:B.
点评:本题考查了直线的倾斜角与斜率的关系、倍角公式,属于基础题.

练习册系列答案
相关题目
已知双曲线中心为坐标原点,焦点在坐标轴上,其图象过点(1,2)且离心率为
,则该双曲线的实轴长为( )
| 2 |
A、
| ||
| B、3 | ||
C、2
| ||
| D、6 |
执行如图所示的程序框图,输出的T的值为( )


| A、12 | B、20 | C、42 | D、30 |
函数y=(a2-3a+1)•ax是指数函数,则a等于( )
| A、a=3 | B、a=3或0 |
| C、a=0 | D、a>0且a≠1 |
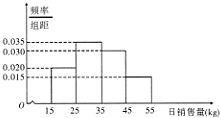 根据市场统计,某商品的日销售量X(单位:kg)的频率分市直方图如图所示,则由频率分布直方图得到该商品日销售量的中位数的估计值为( )
根据市场统计,某商品的日销售量X(单位:kg)的频率分市直方图如图所示,则由频率分布直方图得到该商品日销售量的中位数的估计值为( )| A、35 | B、33.6 |
| C、30.7 | D、28.3 |
若集合S={y|y=3x,x∈R},T={y|y=x,x∈R},则S∩T是( )
| A、S | B、T |
| C、{x|-1≤x<0} | D、∅ |
已知函数f(x)=x3+ax2+bx+a2在x=1处取极值10,则f(0)=( )
| A、9 | B、16 |
| C、9或16 | D、-9或16 |
若曲线y=x2+ax+b在点p(0,b)处的切线方程为x-y+1=0,则a,b的值分别为( )
| A、1,1 | B、-1,1 |
| C、1,-1 | D、-1,-1 |