题目内容
已知O为原点,双曲线
-y2=1上有一点P,过P作两条渐近线的平行线,交点分别为A,B,平行四边形OBPA的面积为1,则双曲线的离心率为( )
| x2 |
| a2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出|OA|,P点到OA的距离,利用平行四边形OBPA的面积为1,求出a,可得c,即可求出双曲线的离心率.
解答:
解:渐近线方程是:x±ay=0,设P(m,n)是双曲线上任一点,
过P平行于OB:x+ay=0的方程是:x+ay-m-an=0与OA方程:x-ay=0交点是A(
,
),
|OA|=|
|
,P点到OA的距离是:d=
∵|OA|•d=1,
∴|
|
•
=1,
∵
-n2=1,
∴a=2,∴c=
,
∴e=
.
故选:C.
过P平行于OB:x+ay=0的方程是:x+ay-m-an=0与OA方程:x-ay=0交点是A(
| m+an |
| 2 |
| m+an |
| 2a |
|OA|=|
| m+an |
| 2 |
1+
|
| |m-an| | ||
|
∵|OA|•d=1,
∴|
| m+an |
| 2 |
1+
|
| |m-an| | ||
|
∵
| m2 |
| a2 |
∴a=2,∴c=
| 5 |
∴e=
| ||
| 2 |
故选:C.
点评:本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
设f(x)=lnx+2x-6,则下列区间中使f(x)=0有实数解的区间是( )
| A、[1,2] |
| B、[2,3] |
| C、[3,4] |
| D、[4,5] |
已知双曲线中心为坐标原点,焦点在坐标轴上,其图象过点(1,2)且离心率为
,则该双曲线的实轴长为( )
| 2 |
A、
| ||
| B、3 | ||
C、2
| ||
| D、6 |
一个几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
| B、10 | ||
| C、30 | ||
D、24+2
|
执行如图所示的程序框图,输出的T的值为( )


| A、12 | B、20 | C、42 | D、30 |
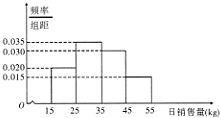 根据市场统计,某商品的日销售量X(单位:kg)的频率分市直方图如图所示,则由频率分布直方图得到该商品日销售量的中位数的估计值为( )
根据市场统计,某商品的日销售量X(单位:kg)的频率分市直方图如图所示,则由频率分布直方图得到该商品日销售量的中位数的估计值为( )| A、35 | B、33.6 |
| C、30.7 | D、28.3 |
点P(a,b)是⊙O:x2+y2=r2(r>0)内一点,直线l1是以P为中点的弦所在直线,l2:ax+by=r2,则有( )
| A、l1⊥l2且l2与⊙O相离 |
| B、l1∥l2且l2与⊙O相离 |
| C、l1∥l2且l2与⊙O相交 |
| D、l1⊥l2且l2与⊙O相切 |