题目内容
规定甲乙两地通话m分钟的电话费由f(m)=1.06×(0.5×[m]+1)(单位:元)给出,其中m>0,记[m]大于或等于m的最小整数(如:[4]=4,[3,8]=4),若从甲地到乙地通话费用为4.24元,则通话时间m的取值范围是( )
| A、(4,5] |
| B、(5,6] |
| C、(6,7] |
| D、(7,8] |
考点:函数模型的选择与应用
专题:计算题,函数的性质及应用
分析:由甲地到乙地通话m分钟的电话费由f(x)=1.06×(0.50×[m]+1),将话费为4.24元代入函数的解析式中,易给出[m]的值,由[m]是大于或等于m的最小整数,我们不难得到通话时间m的取值范围.
解答:
解:∵4.24=1.06(0.50×[m]+1),
∴0.5[m]=3,
∴[m]=6,
∴m∈(5,6].
故选:B.
∴0.5[m]=3,
∴[m]=6,
∴m∈(5,6].
故选:B.
点评:这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
执行如图所示的程序框图,输出的T的值为( )


| A、12 | B、20 | C、42 | D、30 |
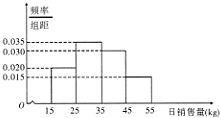 根据市场统计,某商品的日销售量X(单位:kg)的频率分市直方图如图所示,则由频率分布直方图得到该商品日销售量的中位数的估计值为( )
根据市场统计,某商品的日销售量X(单位:kg)的频率分市直方图如图所示,则由频率分布直方图得到该商品日销售量的中位数的估计值为( )| A、35 | B、33.6 |
| C、30.7 | D、28.3 |
若集合S={y|y=3x,x∈R},T={y|y=x,x∈R},则S∩T是( )
| A、S | B、T |
| C、{x|-1≤x<0} | D、∅ |
下列命题中错误的是( )
| A、如果平面α内的任何直线都平行平面β,则α∥β |
| B、如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
| C、如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么直线l⊥平面γ |
| D、如果平面α⊥平面β,α∩β=m,直线n⊥m,则n⊥β |
已知函数f(x)=x3+ax2+bx+a2在x=1处取极值10,则f(0)=( )
| A、9 | B、16 |
| C、9或16 | D、-9或16 |
点P(a,b)是⊙O:x2+y2=r2(r>0)内一点,直线l1是以P为中点的弦所在直线,l2:ax+by=r2,则有( )
| A、l1⊥l2且l2与⊙O相离 |
| B、l1∥l2且l2与⊙O相离 |
| C、l1∥l2且l2与⊙O相交 |
| D、l1⊥l2且l2与⊙O相切 |
已知
=(-3,2),
=(-1,0),若向量λ
+
与
-2
平行,则实数λ的值为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、-
| ||
B、
| ||
C、-
| ||
D、
|