题目内容
在三棱锥A-BCD中，已知AB⊥平面BCD，∠BCD=90°，AB=a，BC=b，CD=c，a2+b2+c2=4，则三棱锥A-BCD的外接球的表面积为（ ）
A、
| ||
B、
| ||
| C、4π | ||
| D、16π |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：由题意，该三棱锥与以a，b，c为从同一顶点出发的三条棱长的长方体又相同的外接球，求出球的半径，即可得出三棱锥A-BCD的外接球的表面积．
解答：
解：由题意，该三棱锥与以a，b，c为从同一顶点出发的三条棱长的长方体又相同的外接球，且球的直径为2R=
=2，所以R=1，所以三棱锥A-BCD的外接球的表面积为4π．
故选：C．
| a2+b2+c2 |
故选：C．
点评：本题考查三棱锥A-BCD的外接球的表面积，考查学生的计算能力，确定球的直径是关键．
练习册系列答案
相关题目
一个几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
| B、10 | ||
| C、30 | ||
D、24+2
|
如图是某一几何体的三视图，则这个几何体的体积是（ ）
| A、8+8π | B、8+2π |
| C、16+8π | D、16+2π |
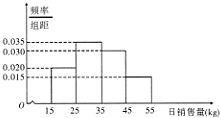根据市场统计，某商品的日销售量X（单位：kg）的频率分市直方图如图所示，则由频率分布直方图得到该商品日销售量的中位数的估计值为（ ）| A、35 | B、33.6 |
| C、30.7 | D、28.3 |
椭圆ax2+by2+ab=0（a＜b＜0）的焦点坐标为（ ）
A、（±
| ||
B、（±
| ||
C、（0．±
| ||
D、（0，±
|
下列命题中错误的是（ ）
| A、如果平面α内的任何直线都平行平面β，则α∥β |
| B、如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β |
| C、如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么直线l⊥平面γ |
| D、如果平面α⊥平面β，α∩β=m，直线n⊥m，则n⊥β |
已知⊙C的圆心C在y=
上，且⊙C过原点，OC交x轴、y轴于另两点A、B，则三角形OAB的面积为（ ）
| 1 |
| x |
| A、1 | B、2 | C、4 | D、8 |
设集合A={-3，-1，0，1，3}，B={x∈N|
∈Z}，则A∩B=（ ）
| 3 |
| 2-x |
| A、{-1，1} |
| B、{1，3} |
| C、{0，1，3} |
| D、{-1，1，3} |