题目内容
若四棱柱的侧面是全等的矩形，则该棱柱是（ ）
| A、长方体 | B、正四棱柱 |
| C、正方体 | D、底面是菱形的直棱柱 |
考点：棱柱的结构特征
专题：空间位置关系与距离
分析：该棱柱的侧棱一定垂直于底面，并且底面一定是菱形，由此能求出结果．
解答：
解：∵四棱柱的侧面是全等的矩形，
∴该棱柱的侧棱一定垂直于底面，并且底面一定是菱形，
∴该棱柱是底面是菱形的直棱柱．
故选：D．
∴该棱柱的侧棱一定垂直于底面，并且底面一定是菱形，
∴该棱柱是底面是菱形的直棱柱．
故选：D．
点评：本题考查棱柱形状的判断，是基础题，解题时要熟练掌握棱柱的性质和分类．
练习册系列答案
相关题目
设f（x）=lnx+2x-6，则下列区间中使f（x）=0有实数解的区间是（ ）
| A、[1，2] |
| B、[2，3] |
| C、[3，4] |
| D、[4，5] |
一个几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
| B、10 | ||
| C、30 | ||
D、24+2
|
执行如图所示的程序框图，输出的T的值为（ ）
| A、12 | B、20 | C、42 | D、30 |
如图是某一几何体的三视图，则这个几何体的体积是（ ）
| A、8+8π | B、8+2π |
| C、16+8π | D、16+2π |
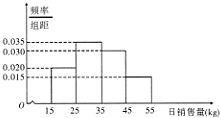根据市场统计，某商品的日销售量X（单位：kg）的频率分市直方图如图所示，则由频率分布直方图得到该商品日销售量的中位数的估计值为（ ）| A、35 | B、33.6 |
| C、30.7 | D、28.3 |
下列命题中错误的是（ ）
| A、如果平面α内的任何直线都平行平面β，则α∥β |
| B、如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β |
| C、如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么直线l⊥平面γ |
| D、如果平面α⊥平面β，α∩β=m，直线n⊥m，则n⊥β |
以线段AB：x+y-2=0（0≤x≤2）为直径的圆的方程为（ ）
| A、（x+1）2+（y+1）2=2 |
| B、（x-1）2+（y-1）2=2 |
| C、（x+1）2+（y+1）2=8 |
| D、（x-1）2+（y-1）2=8 |