Question

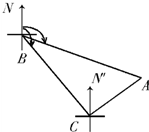如图，货轮在海上以40km/h的速度由B航行到C，航行的方位角∠NBC=140°，A处有灯塔，其方位角∠NBA=110°．在C处观测灯塔A的方位角∠N′CA=35°．由B到C需航行半小时，则C到灯塔A的距离是

 

km．

Answer 1

考点：解三角形的实际应用

专题：解三角形

分析：根据题意分别求得∠CBA，∠BNC进而求得∠A，最后利用正弦定理求得AC．

解答： 解：依题意知∠CBA=140°-110°=30°，
∠BCN′=180°-140°=40°．
∴∠A=180°-30°-75°=75°，
sin75°=sin（30°+45°）=

1

2

×

2

2

+

3

2

×

2

2

=

2 + 6

4

，
BC=40×

1

2

=20km，
在△ABC中

AC

sinB

=

BC

sinA

，
∴AC=

BC

sinA

•sinB=

20

2 + 6 4

×

1

2

=10

6

-10

2

（km）．
答：C到灯塔A的距离是10

6

-10

2

km．
故答案为：10

6

-10

2

点评：本题主要考查了解三角形的实际应用．考查了学生对基础知识的实际运用．