题目内容
若x,y满足约束条件
,且z=kx+y取得最小值的点有无数个,则k= .
|
考点:简单线性规划
专题:探究型,数形结合,不等式的解法及应用
分析:由约束条件作出可行域,化目标函数为直线方程的斜截式,然后分目标函数直线与BC和AB重合得答案.
解答:
解:由目标函数作出可行域如图:

目标函数z=kx+y可化为直线l:y=-kx+z,依题意-k≠0,
当-k>0,即k<0时,当l运动至与BC重合时,最优解有无数个,符合题意,
此时-k=2,得k=-2;
当-k<0,即k>0时,当l运动至与AB重合时,最优解有无数个,符合题意,
此时-k=-1,得k=1.
综上①②可知,k=1或-2.
故答案为:1或-2.

目标函数z=kx+y可化为直线l:y=-kx+z,依题意-k≠0,
当-k>0,即k<0时,当l运动至与BC重合时,最优解有无数个,符合题意,
此时-k=2,得k=-2;
当-k<0,即k>0时,当l运动至与AB重合时,最优解有无数个,符合题意,
此时-k=-1,得k=1.
综上①②可知,k=1或-2.
故答案为:1或-2.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知一元二次函数f(x)=x2+bx+c,且不等式x2+bx+c>0的解集为{x|x<-1或x>
},则f(10x)>0的解集为( )
| 1 |
| 2 |
| A、{x|x<-1或x>lg2} |
| B、{x|-1<x<lg2} |
| C、{x|x>-lg2} |
| D、{x|x<-lg2} |
(文)若a∈R,则“a2>a”是“a>1”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
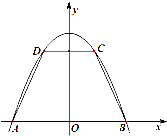 如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S.
如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S.