题目内容
6. 如图,椭圆的中心在坐标原点,A,B为顶点,F为焦点,当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时,此类椭圆称为“黄金椭圆”,可推算出“黄金椭圆”的离心率e=$\frac{\sqrt{5}-1}{2}$.
如图,椭圆的中心在坐标原点,A,B为顶点,F为焦点,当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时,此类椭圆称为“黄金椭圆”,可推算出“黄金椭圆”的离心率e=$\frac{\sqrt{5}-1}{2}$.
分析 在三角形AFB中,分别求出AB,FA,FB,再由勾股定理,结合离心率公式以及范围,解方程即可求得双曲线的离心率.
解答 解:在三角形AFB中,|FB|=$\sqrt{{b}^{2}+{c}^{2}}$,
|AB|=$\sqrt{{a}^{2}+{b}^{2}}$,|FA|=a+c.
由FB⊥AB,则(a+c)2=(b2+a2)+b2+c2=3a2-c2,
整理得c2+ac-a2=0,即e2+2e-2=0,
解得e=$\frac{-1±\sqrt{5}}{2}$,
由于椭圆的0<e<1,
即有e=$\frac{\sqrt{5}-1}{2}$.
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查双曲线的方程和性质,考查离心率的求法,考查勾股定理的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
8.把函数y=cos(2x+φ)(φ>0)的图象上各点的横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),再将图象向右平移$\frac{π}{3}$个单位长度,所得图象关于y轴对称,则φ的最小值为( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
1.下列命题中正确的个数是
①若¬p是q的必要而不充分条件,则p是¬q的充分而不必要条件;
②命题“对任x∈R,都x2≥0”的否定为“存x0∈R,使x02<0”;
③若p∧q为假命题,则p与q均为假命题.( )
①若¬p是q的必要而不充分条件,则p是¬q的充分而不必要条件;
②命题“对任x∈R,都x2≥0”的否定为“存x0∈R,使x02<0”;
③若p∧q为假命题,则p与q均为假命题.( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
15.如图是一个几何体的三视图,则这个几何体的体积是 ( )


| A. | $\frac{57}{2}$ | B. | 27 | C. | 26 | D. | 28 |
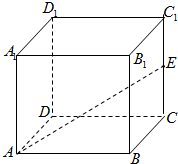 如图,已知正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则AE与平面B1BCC1所成的角为$arctan\frac{{2\sqrt{5}}}{5}$.($arcsin\frac{2}{3}$,$arccos\frac{{\sqrt{5}}}{3}$)(结果用反三角表示)
如图,已知正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则AE与平面B1BCC1所成的角为$arctan\frac{{2\sqrt{5}}}{5}$.($arcsin\frac{2}{3}$,$arccos\frac{{\sqrt{5}}}{3}$)(结果用反三角表示)