题目内容
3.在空间中,“直线a,b没有公共点”是“直线a,b互为异面直线”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 利用空间中两直线的位置关系直接求解.
解答 解:“直线a,b没有公共点”⇒“直线a,b互为异面直线或直线a,b为平行线”,
“直线a,b互为异面直线”⇒“直线a,b没有公共点”,
∴“直线a,b没有公共点”是“直线a,b互为异面直线”的必要不充分条件.
故选:B.
点评 本题考查空间中两直线的位置关系的判断,是基础题,解题时要注意充分条件、必要条件、充要条件的性质的合理运用.

练习册系列答案
相关题目
4.函数y=f(2x)的定义域为[1,2],则函数y=f(log2x)的定义域为( )
| A. | [0,1] | B. | [1,2] | C. | [2,4] | D. | [4,16] |
8.在△ABC中,a,b,c分别是角A,B,C的对边,a=8,b=4,A=60°,则cosB=( )
| A. | $\frac{\sqrt{13}}{4}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | -$\frac{\sqrt{3}}{4}$ | D. | -$\frac{\sqrt{13}}{4}$ |
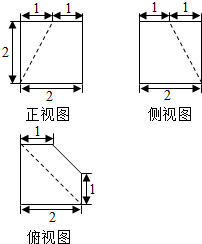
15.如图是一个几何体的三视图,则这个几何体的体积是 ( )


| A. | $\frac{57}{2}$ | B. | 27 | C. | 26 | D. | 28 |
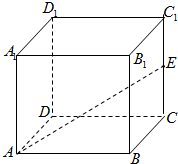 如图,已知正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则AE与平面B1BCC1所成的角为$arctan\frac{{2\sqrt{5}}}{5}$.($arcsin\frac{2}{3}$,$arccos\frac{{\sqrt{5}}}{3}$)(结果用反三角表示)
如图,已知正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则AE与平面B1BCC1所成的角为$arctan\frac{{2\sqrt{5}}}{5}$.($arcsin\frac{2}{3}$,$arccos\frac{{\sqrt{5}}}{3}$)(结果用反三角表示)