题目内容
2．已知函数f（x）是奇函数，且在[0，+∞）上是增函数，不等式f（2x+1）＜f（5）的解集为（ ）| A． | （2，+∞） | B． | （-∞，2） | C． | [2，+∞） | D． | [3，+∞） |
分析 利用函数的单调性以及奇偶性得到自变量的关系，将抽象不等式转化为一元一次不等式解之．
解答 解：因为函数f（x）是奇函数，且在[0，+∞）上是增函数，
所以函数在（-∞，0]也是增函数，
所以不等式f（2x+1）＜f（5）等价于2x+1＜5，解得x＜2；
所以不等式的解集为（-∞，2）．
故选：B
点评 本题考查了运用函数的单调性和奇偶性解抽象不等式；属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
3．在梯形ABCD中，$\overrightarrow{AB}$=3$\overrightarrow{DC}$，则$\overrightarrow{BC}$等于（ ）
| A． | -$\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$ | B． | -$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{4}{3}$$\overrightarrow{AD}$ | C． | -$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AD}$ | D． | -$\frac{2}{3}$$\overrightarrow{AB}$-$\overrightarrow{AD}$ |
4．函数y=f（2x）的定义域为[1，2]，则函数y=f（log2x）的定义域为（ ）
| A． | [0，1] | B． | [1，2] | C． | [2，4] | D． | [4，16] |
8．把函数y=cos（2x+φ）（φ＞0）的图象上各点的横坐标缩短到原来的$\frac{1}{2}$（纵坐标不变），再将图象向右平移$\frac{π}{3}$个单位长度，所得图象关于y轴对称，则φ的最小值为（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{6}$ |
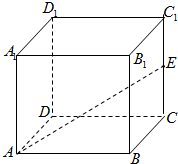如图，已知正方体ABCD-A1B1C1D1，AA1=2，E为棱CC1的中点，则AE与平面B1BCC1所成的角为$arctan\frac{{2\sqrt{5}}}{5}$．（$arcsin\frac{2}{3}$，$arccos\frac{{\sqrt{5}}}{3}$）（结果用反三角表示）