题目内容
16.$\sqrt{3}$×$\root{3}{\frac{3}{2}}$×$\root{6}{12}$+$\frac{8\sqrt{3}}{3}$×($\frac{4}{3}$)${\;}^{-\frac{3}{2}}$=( )| A. | 12 | B. | 9 | C. | 6 | D. | 3 |
分析 根据指数幂的运算法则计算即可.
解答 解:$\sqrt{3}$×$\root{3}{\frac{3}{2}}$×$\root{6}{12}$+$\frac{8\sqrt{3}}{3}$×($\frac{4}{3}$)${\;}^{-\frac{3}{2}}$,
=${3}^{\frac{1}{2}}$•${3}^{\frac{1}{3}}$•${2}^{-\frac{1}{3}}$•$(3×4)^{\frac{1}{6}}$+$8•{3}^{-\frac{1}{2}}$×${2}^{2×(-\frac{3}{2})}$×${3}^{\frac{3}{2}}$,
=${3}^{(\frac{1}{2}+\frac{1}{3}+\frac{1}{6})}$•${2}^{(-\frac{1}{3}+\frac{1}{3})}$+${3}^{(-\frac{1}{2}+\frac{3}{2}})$•23-3,
=3×1+3×1,
=6,
故选:C.
点评 本题考查了指数幂的运算法则,关键考查了学生的运算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.某四面体的三视图如图所示,该四面体外接球的表面积为( )

| A. | 41π | B. | $\frac{41π}{2}$ | C. | 48π | D. | 24π |
4.函数y=f(2x)的定义域为[1,2],则函数y=f(log2x)的定义域为( )
| A. | [0,1] | B. | [1,2] | C. | [2,4] | D. | [4,16] |
8.把函数y=cos(2x+φ)(φ>0)的图象上各点的横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),再将图象向右平移$\frac{π}{3}$个单位长度,所得图象关于y轴对称,则φ的最小值为( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
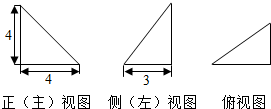
15.如图是一个几何体的三视图,则这个几何体的体积是 ( )


| A. | $\frac{57}{2}$ | B. | 27 | C. | 26 | D. | 28 |