题目内容
16.已知F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点,两条渐近线分别为l1,l2,经过右焦点F2垂直于l1的直线分别交l1,l2于A,B两点,若|OA|+|OB|=2|AB|,且F2在线段AB上,则双曲线的渐近线斜率为( )| A. | $±\frac{{\sqrt{5}}}{2}$ | B. | ±2 | C. | $±\sqrt{2}$ | D. | $±\frac{1}{2}$ |
分析 由已知AB与x轴交于点F2,设∠AOF2=α,则$tanα=\frac{b}{a}$,△AOB中,可得$tan2α=\frac{4}{3}$,$tanα=\frac{1}{2}$,即可求出双曲线的渐近线斜率.
解答 解:由已知AB与x轴交于点F2,设∠AOF2=α,
则$tanα=\frac{b}{a}$,△AOB中,可得$tan2α=\frac{4}{3}$,
设|OA|=m-d、|AB|=m、|OB|=m+d,
∵OA⊥BF,∴(m-d)2+m2=(m+d)2,
整理,得d=$\frac{1}{4}$m,△AOB中,∠AOB=2α,tan∠AOB=tan2α=$\frac{|AB|}{|OA|}$=$\frac{4}{3}$
∴$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{4}{3}$,∴$tanα=\frac{1}{2}$,
∴双曲线的渐近线斜率为$±\frac{1}{2}$.
故选D.
点评 本题考查了双曲线的简单性质,考查学生的计算能力,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
7.若圆台的上、下底面半径的比为3:5,则它的中截面分圆台上下两部分面积之比为( )
| A. | 3:5 | B. | 9:25 | C. | 5:$\sqrt{41}$ | D. | 7:9 |
4.已知正四棱锥P-ABCD的底面边长为$\sqrt{2}$,体积为$\frac{4}{3}$,则此棱锥的内切球与外接球的半径之比为( )
| A. | 1:2 | B. | 2:5 | C. | 1:3 | D. | 4:5 |
11.已知$sinα=\frac{4}{5},α∈({\frac{π}{2},π}),cosβ=-\frac{5}{13},β是第三象限角$.
(1)求sin(α-β)的值
(2)求tan(α+β)的值.
(1)求sin(α-β)的值
(2)求tan(α+β)的值.
5.一质点直线运动的方程为s=t2+1,则在时间[1,2]内的平均速度为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),对于任意实数k,下列直线被椭圆所截弦长与直线y=kx+1被截得的弦长不可能相等是( )
| A. | kx+y+k=0 | B. | kx-y-1=0 | C. | kx+y-k=0 | D. | kx+y-2=0 |
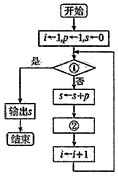 给出30个数:1,2,4,7,…其规律是:第一个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,以此类推,要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),
给出30个数:1,2,4,7,…其规律是:第一个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,以此类推,要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),