题目内容
一次登岛、夺岛军事演习中,红军2000官兵乘军舰登岛,蓝军在登岛海域布置鱼雷反登岛,每搜军舰在登岛过程中被蓝军鱼雷击沉的概率为p(0<p<1),红军现有五艘军舰,每艘军舰最大乘员500人,躲过鱼雷袭击就能成功登岛,登岛官兵至少需要1500人,才能击败夺岛蓝军,成功夺岛,红军可选用两种方案运载官兵:
方案甲:使用4艘军舰.
方案乙:使用5艘军舰,每艘乘员400人.
(1)如果以登岛人数论成败,红军应选择哪种方案?
(2)如果以夺岛论成败,红军应选择哪种方案?
方案甲:使用4艘军舰.
方案乙:使用5艘军舰,每艘乘员400人.
(1)如果以登岛人数论成败,红军应选择哪种方案?
(2)如果以夺岛论成败,红军应选择哪种方案?
考点:概率的应用
专题:应用题,概率与统计
分析:(1)设甲、乙方案躲过鱼雷袭击军舰数量分别为x0,y0,则x0~B(4,q),y0~B(5,q),其中p+q=1,求出EX=EY,DX>DY,即可得出结论;
(2)甲方案红军成功夺岛的概率p1=
q3p+q4,乙方案红军成功夺岛的概率p2=
q4p+q5,作差,即可得出结论.
(2)甲方案红军成功夺岛的概率p1=
| C | 3 4 |
| C | 4 5 |
解答:
解:(1)设甲、乙方案躲过鱼雷袭击军舰数量分别为x0,y0,则x0~B(4,q),y0~B(5,q),其中p+q=1,
∴Ex0=4q,Ey0=5q,Dx0=4pq,Dy0=5pq,
甲、乙方案红军成功登岛人数分别为X=500x0,Y=400y0,则:EX=500Ex0=2000q,EY=400Ey0=2000q,
∴EX=EY,DX=5002Dx0=4×5002pq,DY=4002Dy0=5×4002pq.
∴DX>DY,
∴如果以登岛人数论成败,红军应选择乙方案.
(2)甲方案红军成功夺岛的概率p1=
q3p+q4,乙方案红军成功夺岛的概率p2=
q4p+q5
p1-p2=4q5-8q4+4q3=4q3(q2-2q+1)=4q3(q-1)2>0,
∴p1>p2,
∴如果以夺岛论成败,红军应选择甲方案.
∴Ex0=4q,Ey0=5q,Dx0=4pq,Dy0=5pq,
甲、乙方案红军成功登岛人数分别为X=500x0,Y=400y0,则:EX=500Ex0=2000q,EY=400Ey0=2000q,
∴EX=EY,DX=5002Dx0=4×5002pq,DY=4002Dy0=5×4002pq.
∴DX>DY,
∴如果以登岛人数论成败,红军应选择乙方案.
(2)甲方案红军成功夺岛的概率p1=
| C | 3 4 |
| C | 4 5 |
p1-p2=4q5-8q4+4q3=4q3(q2-2q+1)=4q3(q-1)2>0,
∴p1>p2,
∴如果以夺岛论成败,红军应选择甲方案.
点评:本题考查概率的运用,考查学生利益数学知识解决实际问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=2cos(
-ωx)的最小正周期是4π,则ω等于( )
| π |
| 3 |
| A、2 | ||
B、
| ||
| C、±2 | ||
D、±
|
已知a∈R,“实系数一元二次方程x2+ax+
=0的两根都是虚数”是“存在复数z同时满足|z|=2且|z+a|=1”的( )条件.
| 9 |
| 4 |
| A、充分非必要 |
| B、必要非充分 |
| C、充分必要 |
| D、既非充分又非必要 |
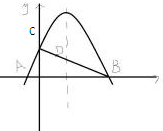 如图,抛物线y=ax2+bx+6与x轴交于AB两点与y轴交点C,已知A(-1,0)、B(3,0).
如图,抛物线y=ax2+bx+6与x轴交于AB两点与y轴交点C,已知A(-1,0)、B(3,0).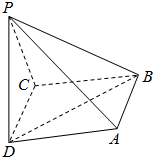 四棱锥P-ABCD的底面是边长为2的正方形,PC=2,PC⊥BC,异面直线AB与PC所成的角为60°.
四棱锥P-ABCD的底面是边长为2的正方形,PC=2,PC⊥BC,异面直线AB与PC所成的角为60°.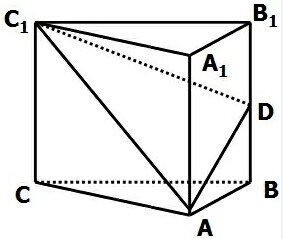 直三棱柱ABC-A1B1C1中,A1A=AC=
直三棱柱ABC-A1B1C1中,A1A=AC=