题目内容
已知椭圆E：
+
=1，点A是椭圆与y轴的交点，F为椭圆的右焦点，直线l与椭圆交于B，C两点．
（1）若点M满足：
=2
，
=
(
+
)．
①求点M的坐标；②求直线l的方程；
（2）设直线l的方程为y=kx+m，若
•
=0，D在BC上，且
•
=0．
①求证：直线l恒过一定点，并求出该定点坐标；②求动点D的轨迹方程．
| x2 |
| 20 |
| y2 |
| 16 |
（1）若点M满足：
| AF |
| FM |
| OM |
| 1 |
| 2 |
| OB |
| OC |
①求点M的坐标；②求直线l的方程；
（2）设直线l的方程为y=kx+m，若
| AB |
| AC |
| AD |
| BC |
①求证：直线l恒过一定点，并求出该定点坐标；②求动点D的轨迹方程．
考点：直线与圆锥曲线的综合问题
专题：计算题,证明题,圆锥曲线中的最值与范围问题
分析：由题意得，a=2
，b=4，c=2；
（1）①写出F（2，0），设点M（x，y）；讨论A的坐标，从而由
=2
求出M的坐标；
②讨论点M的坐标，从而写出直线l的方程，再由点M是线段BC的中点求直线l的方程；
（2）①y=kx+m与与椭圆方程联立消y可得，（4+5k2）x2+10kmx+5m2-80=0，借助韦达定理简化运算，从而求出（k2+1）
+k（m-4）
+（m-4）2=0，从而可求出m的值，从而得到定点；
②若A（0，4），则y=kx-
，设点D（x，y），则由
•
=0可得
•k=-1；化简得到动点D的轨迹方程，同理讨论A（0，-4）时的情况即可．
| 5 |
（1）①写出F（2，0），设点M（x，y）；讨论A的坐标，从而由
| AF |
| FM |
②讨论点M的坐标，从而写出直线l的方程，再由点M是线段BC的中点求直线l的方程；
（2）①y=kx+m与与椭圆方程联立消y可得，（4+5k2）x2+10kmx+5m2-80=0，借助韦达定理简化运算，从而求出（k2+1）
| 5m2-80 |
| 4+5k2 |
| -10km |
| 4+5k2 |
②若A（0，4），则y=kx-
| 4 |
| 9 |
| AD |
| BC |
| y-4 |
| x-0 |
解答：
解：由题意得，a=2
，b=4，c=2；
（1）F（2，0），设点M（x，y）；
①若A（0，4），则
=（2，-4），
=（x-2，y）；
则由
=2
可得，
，
解得，x=3，y=-2；
若A（0，-4），则
=（2，4），
=（x-2，y）；
则由
=2
可得，
，
解得，x=3，y=2；
故点M的坐标为（3，-2）或（3，2）；
∵
=
(
+
)，
∴B、C、M三点共线，且点M是线段BC的中点，
故若M（3，-2），设直线l的方程为y=k（x-3）-2；
与椭圆方程联立消y可得，
（4+5k2）x2-10k（3k+2）x+5（3k+2）2-80=0，
则xB+xC=
=3×2=6，
解得，k=
，
同理，当M（3，2）时，k=-
，
故直线l的方程为
y=
（x-3）-2或y=-
（x-3）+2，
即6x-5y-28=0或6x+5y-28=0，
（2）①证明：y=kx+m与与椭圆方程联立消y可得，
（4+5k2）x2+10kmx+5m2-80=0，
则xB+xC=
，xBxC=
；
若A（0，4），则
=（xB，yB-4），
=（xC，yC-4）；
∵
•
=0
∴xBxC+（yB-4）（yC-4）=0，
即xBxC+k2xBxC+k（m-4）（xB+xC）+（m-4）2=0，
即，（k2+1）
+k（m-4）
+（m-4）2=0，
即m=4或m=-
；
当m=4时，直线l恒过点A，不是要求的直线，
故m=-
；
则直线l恒过定点（0，-
）；
若A（0，-4），同理可得直线l恒过定点（0，
）；
②若A（0，4），则y=kx-
，
设点D（x，y），
则由
•
=0可得，
•k=-1；
化简可得，
k（y-4）+x=0，
即
（y-4）+x=0，
化简可得，x2+y2-
y=
，
若若A（0，-4），同理可得x2+y2+
y=
．
| 5 |
（1）F（2，0），设点M（x，y）；
①若A（0，4），则
| AF |
| FM |
则由
| AF |
| FM |
|
解得，x=3，y=-2；
若A（0，-4），则
| AF |
| FM |
则由
| AF |
| FM |
|
解得，x=3，y=2；
故点M的坐标为（3，-2）或（3，2）；
∵
| OM |
| 1 |
| 2 |
| OB |
| OC |
∴B、C、M三点共线，且点M是线段BC的中点，
故若M（3，-2），设直线l的方程为y=k（x-3）-2；
与椭圆方程联立消y可得，
（4+5k2）x2-10k（3k+2）x+5（3k+2）2-80=0，
则xB+xC=
| 10k(3k+2) |
| 4+5k2 |
解得，k=
| 6 |
| 5 |
同理，当M（3，2）时，k=-
| 6 |
| 5 |
故直线l的方程为
y=
| 6 |
| 5 |
| 6 |
| 5 |
即6x-5y-28=0或6x+5y-28=0，
（2）①证明：y=kx+m与与椭圆方程联立消y可得，
（4+5k2）x2+10kmx+5m2-80=0，
则xB+xC=
| -10km |
| 4+5k2 |
| 5m2-80 |
| 4+5k2 |
若A（0，4），则
| AB |
| AC |
∵
| AB |
| AC |
∴xBxC+（yB-4）（yC-4）=0，
即xBxC+k2xBxC+k（m-4）（xB+xC）+（m-4）2=0，
即，（k2+1）
| 5m2-80 |
| 4+5k2 |
| -10km |
| 4+5k2 |
即m=4或m=-
| 4 |
| 9 |
当m=4时，直线l恒过点A，不是要求的直线，
故m=-
| 4 |
| 9 |
则直线l恒过定点（0，-
| 4 |
| 9 |
若A（0，-4），同理可得直线l恒过定点（0，
| 4 |
| 9 |
②若A（0，4），则y=kx-
| 4 |
| 9 |
设点D（x，y），
则由
| AD |
| BC |
| y-4 |
| x-0 |
化简可得，
k（y-4）+x=0，
即
y+
| ||
| x |
化简可得，x2+y2-
| 32 |
| 9 |
| 16 |
| 9 |
若若A（0，-4），同理可得x2+y2+
| 32 |
| 9 |
| 16 |
| 9 |
点评：本题考查了圆锥曲线的综合应用，无论化简与思路都比较困难，属于难题．
练习册系列答案
相关题目
已知全集U={x∈N|x≤4}，A={1，2}，则∁UA为（ ）
| A、{3} |
| B、{0，3} |
| C、{3，4} |
| D、{0，3，4} |
函数y=2cos（
-ωx）的最小正周期是4π，则ω等于（ ）
| π |
| 3 |
| A、2 | ||
B、
| ||
| C、±2 | ||
D、±
|
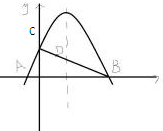如图，抛物线y=ax2+bx+6与x轴交于AB两点与y轴交点C，已知A（-1，0）、B（3，0）．
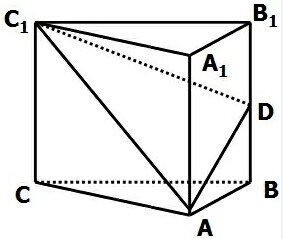直三棱柱ABC-A1B1C1中，A1A=AC=