题目内容
15.已知P(x,y)为区域$\left\{\begin{array}{l}{y^2}-4{x^2}≤0\\ a≤x≤0\end{array}\right.$内的任意一点,当该区域的面积为4时,z=x-2y的最小值是( )| A. | $-5\sqrt{2}$ | B. | $-3\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | 0 |
分析 由约束条件作出可行域,求出使可行域面积为4的a值,化目标函数为直线方程的斜截式,数形结合可得最优解,求出最优解的坐标,代入目标函数得答案
解答 解:由已知不等式得到可行域如图: 由图可得A(a,2a),B(a,-2a),
由图可得A(a,2a),B(a,-2a),
由${S}_{△OAB}=\frac{1}{2}|AB|×|a|$=2a2=4,解得a=-$\sqrt{2}$.
∴A($-\sqrt{2}$,-2$\sqrt{2}$),B($-\sqrt{2}$,2$\sqrt{2}$),
化目标函数z=x-2y为y=$\frac{1}{2}$x-$\frac{1}{2}$z,
∴当y=$\frac{1}{2}$x-$\frac{1}{2}$z过B点时,z最小值$-\sqrt{2}-4\sqrt{2}=-5\sqrt{2}$;
故选:A.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.给定两个命题p,q,“¬(p∨q)为假”是“p∧q为真”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.△ABC内角A,B,C所对的边分别是a,b,c,则“acosA=bcosB”是“A=B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
5.已知tanx=-$\frac{1}{2}$,则2sinxcosx=( )
| A. | -$\frac{4}{5}$ | B. | -3 | C. | -$\frac{7}{5}$ | D. | -$\frac{11}{5}$ |
2.已知集合A={x|(x-6)(x+2)<0},B={x|x-1>0},则A∩B等于( )
| A. | (1,6) | B. | (-1,6) | C. | (-2,1) | D. | (-1,2) |
3.把函数f(x)=$\sqrt{3}$cos2x-sin2x的图象向右平移$\frac{π}{12}$个单位得到函数y=g(x)的图象,则函数y=g(x)在下列哪个区间是单调递减的( )
| A. | [-$\frac{π}{2}$,0] | B. | [-π,0] | C. | [-$\frac{π}{4}$,$\frac{π}{4}$] | D. | [0,$\frac{π}{2}$] |
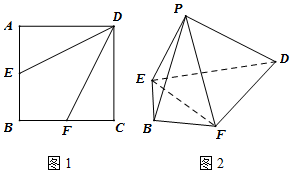 如图1,边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P如图2.
如图1,边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P如图2.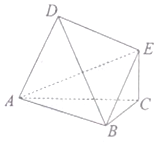 如图△ABC和△ABD均为等腰直角三角形,AD⊥BD,AC⊥BC,平面ABC⊥平面ABD,EC⊥平面ABC,EC=1,$AD=2\sqrt{2}$.
如图△ABC和△ABD均为等腰直角三角形,AD⊥BD,AC⊥BC,平面ABC⊥平面ABD,EC⊥平面ABC,EC=1,$AD=2\sqrt{2}$.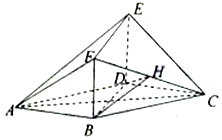 如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.
如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.