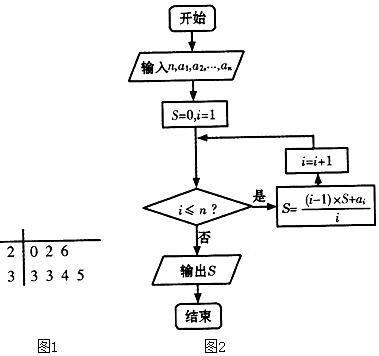
题目内容
3.△ABC中,角A,B,C的对边分别为a,b,c,且三角形的面积S=$\frac{\sqrt{3}}{2}$accosB.(1)求角B的大小;
(2)若a=2$\sqrt{15}$,点D在AB的延长线上,且AD=3,cos∠ADC=$\frac{2}{3}$,求b的值.
分析 (1)由已知利用三角形面积公式,同角三角函数基本关系式可求tanB=$\sqrt{3}$,由特殊角的三角函数值即可得解B的值.
(2)由已知可求∠CBD=$\frac{2π}{3}$,sin∠ADC=$\frac{\sqrt{5}}{3}$,由正弦定理解得CD,进而在△ADC中,由余弦定理可得b的值.
解答 (本题满分为12分)
解:(1)∵S=$\frac{\sqrt{3}}{2}$accosB=$\frac{1}{2}$acsinB,
∴tanB=$\sqrt{3}$,
∴B=$\frac{π}{3}$.
(2)如图,∵B=$\frac{π}{3}$.∴∠CBD=$\frac{2π}{3}$,
∵cos∠ADC=$\frac{2}{3}$,∴sin∠ADC=$\sqrt{1-co{s}^{2}∠ADC}$=$\frac{\sqrt{5}}{3}$,
∴在△BCD中,由正弦定理$\frac{CD}{sin∠CBD}=\frac{BC}{sin∠BDC}$,可得:$\frac{CD}{sin\frac{2π}{3}}=\frac{2\sqrt{15}}{\frac{\sqrt{5}}{3}}$,解得:CD=9,
∴在△ADC中,由余弦定理可得:b2=AD2+CD2-2AD•CD•cos∠ADC=9+81-2×$3×9×\frac{2}{3}$=54.
∴b=3$\sqrt{6}$.
点评 本题主要考查了三角形面积公式,同角三角函数基本关系式,特殊角的三角函数值,正弦定理,余弦定理在解三角形中的综合应用,考查了转化思想和数形结合思想,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
14.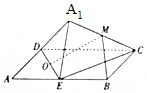 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )| A. | 与平面A1DE垂直的直线必与直线BM垂直 | |
| B. | 异面直线BM与A1E所成角是定值 | |
| C. | 一定存在某个位置,使DE⊥MO | |
| D. | 三棱锥A1-ADE外接球半径与棱AD的长之比为定值 |
18.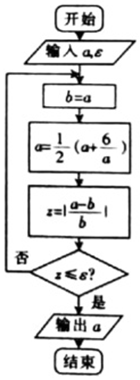 十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法,相较于二分法更具优势,如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图,若输入a=2,?=0.02,则输出的结果为( )
十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法,相较于二分法更具优势,如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图,若输入a=2,?=0.02,则输出的结果为( )
 十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法,相较于二分法更具优势,如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图,若输入a=2,?=0.02,则输出的结果为( )
十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法,相较于二分法更具优势,如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图,若输入a=2,?=0.02,则输出的结果为( )| A. | 3 | B. | 2.5 | C. | 2.45 | D. | 2.4495 |
8.已知各项均不相等的等比数列{an}中,a2=1,且$\frac{1}{4}$a1,a3,$\frac{7}{4}$a5成等差数列,则a4等于( )
| A. | $\frac{1}{49}$ | B. | 49 | C. | $\frac{1}{7}$ | D. | 7 |