题目内容
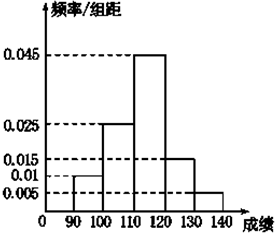 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.(1)求这组数据的样本容量及平均数M;
(2)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成帮扶学习小组.若选出的两人成绩之差大于20,则称这两人为“黄金搭档组”,试求选出的两人为“黄金搭档组”的概率.
考点:频率分布直方图,古典概型及其概率计算公式
专题:概率与统计
分析:(1)根据频率分布直方图,利用公式频率=
求出样本的容量,再求出平均数;
(2)利用列举法写出从第一组和第五组中任意选出两人共有的基本事件数,选出的两人为“黄金搭档组”的基本事件数,求出概率来.
| 频数 |
| 样本容量 |
(2)利用列举法写出从第一组和第五组中任意选出两人共有的基本事件数,选出的两人为“黄金搭档组”的基本事件数,求出概率来.
解答:
解:(1)设90~140分之间的人数为n,
由130~140分数段的人数为2,知0.005×10×n=2,得n=40;
即此样本的容量为40;--(2分)
平均数M=95×0.1+105×0.25+115×0.45+125×0.15+135×0.05=113;--(5分)
(2)依题意第一组共有40×0.01×10=4人,记作A1,A2,A3,A4;
第五组共有2人,记作B1,B2;
从第一组和第五组中任意选出两人共有下列15种选法:
{A1,A2},{A1,A3},{A1,A4},{A1,B1},{A1,B2},
{A2,A3},{A2,A4},{A2,B1},{A2,B2},
{A3,A4},{A3,B1},{A3,B2},
{A4,B1},{A4,B2},
{B1,B2};
设事件A:选出的两人为“黄金搭档组”,
若两人成绩之差大于20,则两人分别来自第一组和第五组,共有8种选法:
{A1,B1},{A2,B1},{A3,B1},{A4,B1},
{A1,B2},{A2,B2},{A3,B2},{A4,B2},
∴P(A)=
.---(12分)
由130~140分数段的人数为2,知0.005×10×n=2,得n=40;
即此样本的容量为40;--(2分)
平均数M=95×0.1+105×0.25+115×0.45+125×0.15+135×0.05=113;--(5分)
(2)依题意第一组共有40×0.01×10=4人,记作A1,A2,A3,A4;
第五组共有2人,记作B1,B2;
从第一组和第五组中任意选出两人共有下列15种选法:
{A1,A2},{A1,A3},{A1,A4},{A1,B1},{A1,B2},
{A2,A3},{A2,A4},{A2,B1},{A2,B2},
{A3,A4},{A3,B1},{A3,B2},
{A4,B1},{A4,B2},
{B1,B2};
设事件A:选出的两人为“黄金搭档组”,
若两人成绩之差大于20,则两人分别来自第一组和第五组,共有8种选法:
{A1,B1},{A2,B1},{A3,B1},{A4,B1},
{A1,B2},{A2,B2},{A3,B2},{A4,B2},
∴P(A)=
| 8 |
| 15 |
点评:本题考查了频率分布直方图的应用问题,也考查了求古典概型的概率问题,是基础题目.

练习册系列答案
相关题目
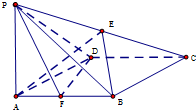 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.