题目内容
函数F(x)=(x2+
)2013+(x+
)2013在区间(0,
]上的最小值为 .
| 1 |
| x |
| 1 |
| x2 |
| 3 |
| 2 |
考点:基本不等式
专题:计算题,不等式的解法及应用
分析:用两次基本不等式求最小值.
解答:
解:F(x)=(x2+
)2013+(x+
)2013≥2
=2
≥2
=22014.
(当且仅当(x2+
)2013=(x+
)2013,且x3=
,即x=1时,等号成立).
故答案为:22014.
| 1 |
| x |
| 1 |
| x2 |
(x2+
|
=2
(2+x3+
|
| (2+2)2013 |
(当且仅当(x2+
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x3 |
故答案为:22014.
点评:本题考查了基本不等式的应用,注意验证不等式等号成立的条件,属于基础题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知命题正确的个数是( )
①若
•
=0,则
=
或
=
;
②(
•
)•
=
•(
•
);
③若
•
=
•
(
≠
),则
=
;
④
•
=
•
;
⑤若
与
不共线,则
与
的夹角为锐角.
①若
| a |
| b |
| a |
| 0 |
| b |
| 0 |
②(
| a |
| b |
| c |
| a |
| b |
| c |
③若
| a |
| b |
| b |
| c |
| b |
| 0 |
| a |
| c |
④
| a |
| b |
| b |
| a |
⑤若
| a |
| b |
| a |
| b |
| A、1 | B、2 | C、3 | D、4 |
已知α是锐角,则下列各式成立的是( )
A、sinα+cosα=
| ||
| B、sinα+cosα=1 | ||
C、sinα+cosα=
| ||
D、sinα+cosα=
|
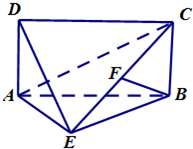 如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.




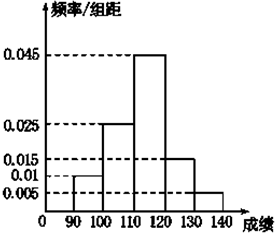 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.