题目内容
若x（2x2-2x-1）+3=（x+1）f（x），且f（x）≥m对一切x∈R恒成立，则实数m的取值范围是 ．
考点：函数恒成立问题
专题：函数的性质及应用
分析：由已知得2（x+1）（x2-x+1）-2（x+1）（x-1）-（x+1）=（x+1）f（x），从而f（x）=2x2-2x+x-2x+2-1=2x2+x+1，由此利用配方法能求出结果．
解答：
解：∵x（2x2-2x-1）+3=（x+1）f（x），
∴2x3+2-2x2+2-x-1=（x+1）f（x），
∴2（x+1）（x2-x+1）-2（x+1）（x-1）-（x+1）=（x+1）f（x），
∴f（x）=2x2-2x+x-2x+2-1=2x2+x+1，
=2（x+
）2+
≥
．
∵f（x）≥m对一切x∈R恒成立，
∴m≤
．
故答案为：m≤
．
∴2x3+2-2x2+2-x-1=（x+1）f（x），
∴2（x+1）（x2-x+1）-2（x+1）（x-1）-（x+1）=（x+1）f（x），
∴f（x）=2x2-2x+x-2x+2-1=2x2+x+1，
=2（x+
| 1 |
| 4 |
| 7 |
| 8 |
| 7 |
| 8 |
∵f（x）≥m对一切x∈R恒成立，
∴m≤
| 7 |
| 8 |
故答案为：m≤
| 7 |
| 8 |
点评：本题考查实数的取值范围的求法，是中档题，解题时要认真审题，注意二次函数的性质的合理运用．
练习册系列答案
相关题目
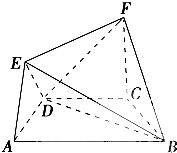在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF=1，
如图所示的四棱锥P-ABCD中，底面ABCD为菱形，PA⊥平面ABCD，E为PC的中点，求证：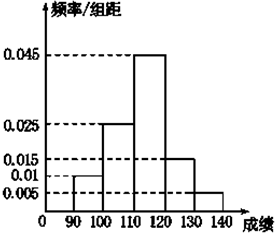
某校高三数学竞赛初赛考试后，对90分以上（含90分）的成绩进行统计，其频率分布直方图如图所示．若130～140分数段的人数为2人．