题目内容
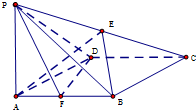 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.(1)求证:BE∥平面PDF;
(2)求二面角E-AB-D的大小.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)取PD的中点M,由已知得四边形MEBF是平行四边形,由此能证明BE∥平面PDF.
(2)以A为原点,AD为y轴,AP为z轴,建立空间直角坐标系,利用同向量法能求出二面角E-AB-D的大小.
(2)以A为原点,AD为y轴,AP为z轴,建立空间直角坐标系,利用同向量法能求出二面角E-AB-D的大小.
解答:
(1)证明:取PD的中点M,
∵E是PC的中点
∴ME是△PCD的中位线,
∴ME
CD,
∵底面ABCD是菱形,F是AB的中点,
∴ME∥FB,且ME=FB,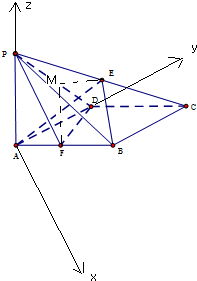
∴四边形MEBF是平行四边形
∴BE∥MF
∵BE∥平面PDF,
MF?平面PDF
∴BE∥平面PDF.
(2)以A为原点,AD为y轴,AP为z轴,建立空间直角坐标系,
由题意知P(0,0,1),C(
,3,0),E(
,
,
),
A(0,0,0),B(
,1,0),D(0,2,0),
=(
,1,0),
=(
,
,
),
=(0,2,0),
平面BAD的法向量
=(0,0,1),
设平面ABE的法向量
=(x,y,z),
则
,
取x=
,得
=(
,-3,6),
∴cos<
,
>=
=
∴二面角E-AB-D的大小为30°.
∵E是PC的中点
∴ME是△PCD的中位线,
∴ME
| ∥ |
. |
| 1 |
| 2 |
∵底面ABCD是菱形,F是AB的中点,
∴ME∥FB,且ME=FB,

∴四边形MEBF是平行四边形
∴BE∥MF
∵BE∥平面PDF,
MF?平面PDF
∴BE∥平面PDF.
(2)以A为原点,AD为y轴,AP为z轴,建立空间直角坐标系,
由题意知P(0,0,1),C(
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
A(0,0,0),B(
| 3 |
| AB |
| 3 |
| AE |
| ||
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| AD |
平面BAD的法向量
| n |
设平面ABE的法向量
| m |
则
|
取x=
| 3 |
| m |
| 3 |
∴cos<
| m |
| n |
| 6 | ||
|
| ||
| 2 |
∴二面角E-AB-D的大小为30°.
点评:本题考查直线与平面平行的证明,考查二面角的大小的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
已知α是锐角,则下列各式成立的是( )
A、sinα+cosα=
| ||
| B、sinα+cosα=1 | ||
C、sinα+cosα=
| ||
D、sinα+cosα=
|
 如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点,求证:
如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点,求证: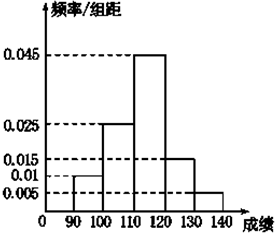 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.