题目内容
已知数列{an}的前n项和为Sn,满足an+Sn=2n,
(1)求an;
(Ⅱ)设bn=(2-n)(an-2),若对任意的正整数n,均有bn∈(-∞,m),求实数m的取值范围.
(1)求an;
(Ⅱ)设bn=(2-n)(an-2),若对任意的正整数n,均有bn∈(-∞,m),求实数m的取值范围.
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)根据an+Sn=2n,令n=1可求a1,n≥2时得an-1+Sn-1=2(n-1),两式相减得an=
an-1+1,再构造新的等比数列{an-2},由等比数列的通项公式求通项an;
(Ⅱ)由(Ⅰ)求出an代入bn=(2-n)(an-2)化简,再化简bn+1-bn并判断出符号及对应的n的范围,可得数列{bn}中项的变化情况,从而求出数列中最大的项,根据条件和恒成立问题,可求出实数m的范围.
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)求出an代入bn=(2-n)(an-2)化简,再化简bn+1-bn并判断出符号及对应的n的范围,可得数列{bn}中项的变化情况,从而求出数列中最大的项,根据条件和恒成立问题,可求出实数m的范围.
解答:
解:(Ⅰ)依题意得,an+Sn=2n,
当n=1时,a1+S1=2,∴a1=1,
当n≥2时,an+Sn=2n,an-1+Sn-1=2(n-1),
两式相减得,2an-an-1=2,则an=
an-1+1,
令an+k=
(an-1+k),即an=
an-1-
k,解得k=-2,
所以
=
,且a1-2=-1
所以数列{an-2}是以-1为首项,以
为公比的等比数列,
则an-2=(-1)×(
)n-1=-
,即an=-
+2;
(Ⅱ)由(Ⅰ)得,bn=(2-n)(an-2)=(n-2)•
,
所以bn+1-bn=
-
=
,
则当n≤3时,bn+1>bn;当n>4时,bn+1<bn,
所以b1<b2<b3=b4>b5>…>bn>…,
即bn有最大值b3=b4=
,
因为对任意的正整数n,均有bn∈(-∞,m),
即bn<m对任意的正整数n都成立,所以m>
,
故实数m的取值范围是m>
.
当n=1时,a1+S1=2,∴a1=1,
当n≥2时,an+Sn=2n,an-1+Sn-1=2(n-1),
两式相减得,2an-an-1=2,则an=
| 1 |
| 2 |
令an+k=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以
| an-2 |
| an-1-2 |
| 1 |
| 2 |
所以数列{an-2}是以-1为首项,以
| 1 |
| 2 |
则an-2=(-1)×(
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
(Ⅱ)由(Ⅰ)得,bn=(2-n)(an-2)=(n-2)•
| 1 |
| 2n-1 |
所以bn+1-bn=
| n-1 |
| 2n |
| n-2 |
| 2n-1 |
| 3-n |
| 2n |
则当n≤3时,bn+1>bn;当n>4时,bn+1<bn,
所以b1<b2<b3=b4>b5>…>bn>…,
即bn有最大值b3=b4=
| 1 |
| 4 |
因为对任意的正整数n,均有bn∈(-∞,m),
即bn<m对任意的正整数n都成立,所以m>
| 1 |
| 4 |
故实数m的取值范围是m>
| 1 |
| 4 |
点评:本题考查了数列an与Sn的关系,利用构造法求数列的通项公式,数列的项的变化趋势,以及恒成立问题转化为求数列的最大项问,注意构造法和等价转化思想的合理运用,试题具有一定的综合性.

练习册系列答案
相关题目
 如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点,求证:
如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点,求证: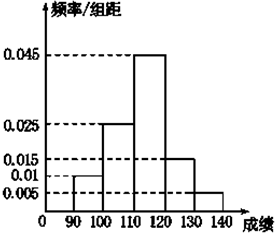 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.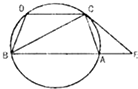 如图,已知圆上的弧
如图,已知圆上的弧