题目内容
9.在等差数列{an}中,a2=3,a3+a6=11(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=an+$\frac{1}{{2}^{{a}_{n}}}$,其中n∈N*,求数列{bn}的前n项和Sn.
分析 (Ⅰ)设等差数列{an}的公差为d,由a2=3,a3+a6=11,可得a1+d=3,2a1+7d=11,联立解出即可得出.
(Ⅱ)bn=an+$\frac{1}{{2}^{{a}_{n}}}$=n+1+$\frac{1}{{2}^{n+1}}$,利用等差数列与等比数列的求和公式即可得出.
解答 解:(Ⅰ)设等差数列{an}的公差为d,∵a2=3,a3+a6=11,
∴a1+d=3,2a1+7d=11,解得a1=2,d=1.
所以数列{an}的通项公式为an=2+(n-1)=n+1.
(Ⅱ)bn=an+$\frac{1}{{2}^{{a}_{n}}}$=n+1+$\frac{1}{{2}^{n+1}}$,
∴Sn=[2+3+…+(n+1)]+$(\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n+1}})$
=$\frac{n(n+3)}{2}$+$\frac{\frac{1}{4}[1-(\frac{1}{2})^{n}]}{1-\frac{1}{2}}$
=$\frac{{n}^{2}+3n+1}{2}$-$\frac{1}{{2}^{n+1}}$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.一个几何体的三视图如图所示,则这个几何体的直观图为( )
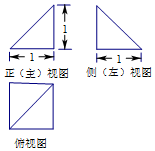

| A. | 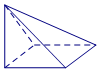 | B. | 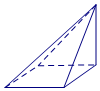 | C. | 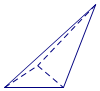 | D. | 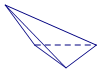 |
17.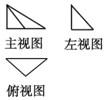 一个高为2的三棱锥的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积( )
一个高为2的三棱锥的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积( )
 一个高为2的三棱锥的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积( )
一个高为2的三棱锥的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积( )| A. | 12π | B. | 9π | C. | $4\sqrt{3}π$ | D. | $\sqrt{3}π$ |
18.函数f(x)=($\frac{1}{2}$)x-x-2的零点所在的区间为( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
18.某四棱锥的三视图如图所示,该四棱锥的表面积为( )


| A. | $1+\sqrt{2}$ | B. | 3 | C. | $2+\sqrt{2}$ | D. | 4 |
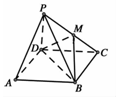 已知四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M在边PC上
已知四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M在边PC上