题目内容
12．已知a，b，c为正实数，$\frac{1}{{a}^{3}}$+$\frac{1}{{b}^{3}}$+$\frac{1}{{c}^{3}}$+27abc的最小值为m，解关于x的不等式|x+l|-2x＜m．分析 根据基本不等式的性质求出m的值，从而解不等式即可．
解答 解：因为a，b，c＞0，
所以$\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}+27abc≥3\root{3}{{\frac{1}{a^3}•\frac{1}{b^3}•\frac{1}{c^3}}}+27abc$
=$\frac{3}{abc}+27abc$$≥2\sqrt{\frac{3}{abc}•27abc}=18$，
当且仅当$a=b=c=\root{3}{{\frac{1}{3}}}$时，取“=”，
所以m=18．…（6分）
所以不等式|x+1|-2x＜m即|x+1|＜2x+18，
所以-2x-18＜x+1＜2x+18，解得$x＞-\frac{19}{3}$，
所以原不等式的解集为$（-\frac{19}{3}，+∞）$．…（10分）
点评 本题考查了基本不等式的性质，考查解不等式问题，是一道基础题．
练习册系列答案
相关题目
2．
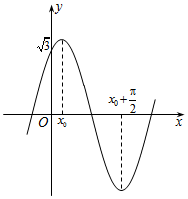已知函数$f（x）=2sin（ωx+φ）（ω＞0，|φ|＜\frac{π}{2}）$的图象如图所示，则函数f（x）的解析式的值为（ ）
已知函数$f（x）=2sin（ωx+φ）（ω＞0，|φ|＜\frac{π}{2}）$的图象如图所示，则函数f（x）的解析式的值为（ ）| A． | $f（x）=2sin（2x+\frac{π}{6}）$ | B． | $f（x）=2sin（2x+\frac{π}{3}）$ | C． | $f（x）=2sin（x+\frac{π}{6}）$ | D． | $f（x）=2sin（x+\frac{π}{3}）$ |
17．
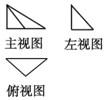一个高为2的三棱锥的三视图如图所示，其中俯视图是一个腰长为2的等腰直角三角形，则该几何体外接球的体积（ ）
一个高为2的三棱锥的三视图如图所示，其中俯视图是一个腰长为2的等腰直角三角形，则该几何体外接球的体积（ ）| A． | 12π | B． | 9π | C． | $4\sqrt{3}π$ | D． | $\sqrt{3}π$ |
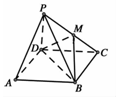已知四棱锥P-ABCD的底面为平行四边形，PD⊥平面ABCD，M在边PC上