Question

已知直线y=x+b与曲线x²+y²=1（x＞0）有交点，则（　　）

• A、-1＜b＜1
• B、-1＜b＜

  2

• C、-

  2

  ≤b≤

  2

• D、-

  2

  ≤b＜1

Answer 1

考点：直线与圆的位置关系

专题：直线与圆

分析：分别画出直线y=x+b与曲线x²+y²=1（x＞0）．当直线经过点（0，1）时，直线与曲线没有公共点．当直线与曲线相切时，直线与曲线有公共点，利用点的直线距离公式和切线的性质即可得出

解答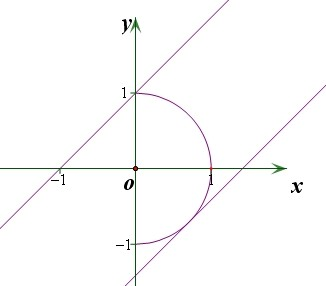： 解：如图所示，当直线经过点（0，1）时，
直线y=x+b与曲线x²+y²=1（x＞0）没有交点，
所以b＜1．
当直线y=x+b与曲线x²+y²=1（x＞0）相切时，
直线与曲线有交点，
由点的直线距离公式可得 
 d=

|b|

2

=1                                                                              
∴b=±

2

                                                                                 
由图可知，应取b=-

2

因此，当-

2

≤b＜1 时，直线y=x+b与曲线x²+y²=1（x＞0）有交点．
故选D．

点评：本题考查了直线与圆的位置关系、相切的性质、数形结合等基础知识与基本技能