题目内容
如图是某人在5天中每天加工零件个数的茎叶图，则该组数据的方差为（ ）A、
| ||
| B、2 | ||
C、
| ||
| D、10 |
考点：极差、方差与标准差,茎叶图
专题：概率与统计
分析：根据该组数据，结合方差计算公式算出该组数据的平均数以及方差，即得正确答案．
解答：
解：该组数据的平均数为=
（18+19+20+21+22）=20
样本方差为
[（18-20）2+（19-20）2+（20-20）2+（21-20）2+（22-20）2]=2，
故选：B
| 1 |
| 5 |
样本方差为
| 1 |
| 5 |
故选：B
点评：本题给出茎叶图，要我们求出数据的平均数和方差，属于基础题．
练习册系列答案
相关题目
不等式2x2+mx+n＞0的解集是{x|x＞3或x＜-2}，则二次函数y=2x2+mx+n的表达式是（ ）
| A、y=2x2+2x+12 |
| B、y=2x2-2x+12 |
| C、y=2x2+2x-12 |
| D、y=2x2-2x-12 |
所有与角α终边相同的角，连同角α在内，可构成的一个集合S是（ ）
| A、{β|β=α+k•180°，k∈Z} |
| B、{β|β=α+k•360°，k∈Z} |
| C、{β|β=α+k•180°，k∈R} |
| D、{β|β=α+k•360°，k∈R} |
若16-x2≥0，则（ ）
| A、0≤x≤4 |
| B、-4≤x≤0 |
| C、-4≤x≤4 |
| D、x≤-4或x≥4 |
已知直线y=x+b与曲线x2+y2=1（x＞0）有交点，则（ ）
| A、-1＜b＜1 | ||||
B、-1＜b＜
| ||||
C、-
| ||||
D、-
|
已知f（x）是定义在R上的偶函数，且对任意x∈R，总有f（x+2）=-f（x）成立，则f（19）=（ ）
| A、-2 | B、-1 | C、0 | D、19 |
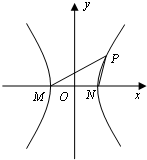已知双曲线x2-y2=2013的左、右顶点分别为M、N，点P是双曲线上异于M、N的任意一点．